Поисковые адаптивные САУ

Самонастраивающиеся адаптивные системы с автоматической оптимизацией критерия качества управления

Задается некоторый критерий качества J и система настраивается так, чтобы выполнялось условие 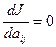. В зависимости от оптимизации алгоритма адаптации различают:

поисковые и беспоисковые адаптивные системы.

В поисковых системах автоматическое поддержание критерия качества обеспечивается итерационными методами, а в беспоисковых системах поддержание критерия обеспечивается путем аналитического решения критерия качества.

Пусть дана исходная САУ и пределен критерий оптимальности 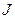как функция некоторых параметров 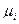, в качестве параметров могут быть рассмотрены как координаты объекта управления, так и задающие и управляющие воздействия.

Известно, что экстремальное значение критерия достигается при условии:

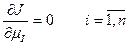
Однако часто аналитически это уравнения решить либо сложно, либо невозможно, поэтому нп практике применяются итерационные (численные) методы, обеспечивающие:

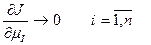
К итерационным методам относятся:

1) Метод Гаусса – Зейделя;

2) Градиентный метод;

3) Наискорейшего спуска

8.4.2.1. Метод Гаусса – Зейделя

В основе метода лежит исследование производной 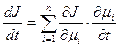в точке экстремума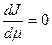

Метод Гаусса-Зейделя предполагает поочередное изменение и определение частных экстремумов 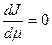при фиксировании всех остальных переменных. Такой цикл повторяется до нахождения экстремума по всем переменным с заданной точностью.

Пример

Пусть критерий оптимальности задан следующей формулой:

Необходимо найти минимум J при начальных значениях

Фиксируем переменную 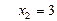и находим частный экстремум по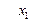

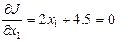
Фиксируем переменную 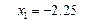и находим частный экстремум по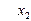

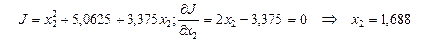
И так далее до тех пор, пока

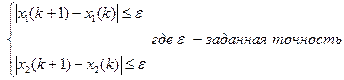
Дата добавления: 2014-01-07