
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Прямая линия на плоскости
|
|
|
|
Лекция №10
Щеточное шлифование
Используемый абразивный инструмент
Различные модификации щеточных шлифовальных элементов:
Диск типа "fladder" или "Quick Disk" – это многолучевая звезда из шлифовальной шкурки на тканевой основе с пенопластовыми прокладками, обеспечивающими правильное позиционирование дисков относительно друг друга.
Шлифовальные щетки – основа этого инструмента является центральная втулка, в которую вставляются шлифовальные щетки. Сами щетки состоят из следующих элементов:
· основа – пластиковая основа для крепления к центральной втулке;
· шлифовальная шкурка – эластичная шлифовальная шкурка, нарезанная на лепестки;
· щетина – может быть выполнена из сизаля или лески.
Торцевой щеточный элемент – данный тип шлифовального элемента состоит из щеточных сегментов закрепленных на диск, осуществляющий вращательные движения в одной плоскости с обрабатываемой поверхностью.
Оборудование
Шлифовальные элементы типа "fladder" - "Quick Disk" или "Quick Flex" могут применяться как с ручным инструментом, так и на промышленных станках. Торцевой щеточный элемент применяется только для работы на станках.
Щеточные шлифовальные элементы не требуют профилирования, проникновение в глубину обрабатываемого профиля достигается за счет их разбивки на отдельные сегменты (лепестки шлифовальной ткани).
Прямая линия на плоскости может быть задана:
1. Векторным уравнением в параметрической форме.
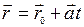 ,
, 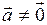 , (1)
, (1)
где 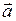 - направляющий вектор прямой,
- направляющий вектор прямой, 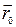 - радиус-вектор фиксированной точки на прямой.
- радиус-вектор фиксированной точки на прямой.
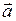
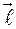
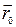
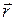
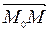
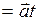 , точка
, точка 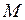 - текущая точка прямой
- текущая точка прямой 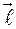 .
.
2. Нормальным векторным уравнением
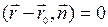 ,
, 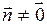 , (2)
, (2)
где 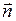 - нормальный вектор прямой.
- нормальный вектор прямой.
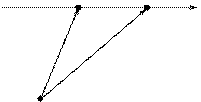
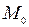
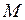
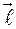
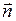
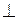
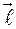
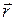
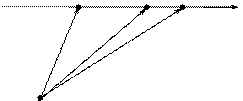
3. Уравнение прямой, проходящей через две различные точки, может быть записано в векторной форме.
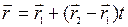 . (3)
. (3)
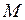
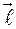
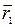
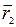
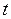 - параметр,
- параметр, 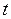
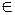 R.
R.
Когда 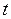 пробегает от
пробегает от 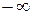 до
до 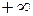 , тогда точка М пробегает всю прямую
, тогда точка М пробегает всю прямую 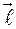 .
.
4. Общее уравнение прямой на плоскости. Уравнение вида
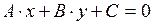 (4)
(4)
называется общим уравнением прямой.
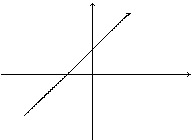
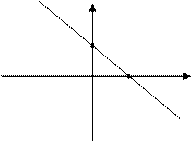
5. Уравнение
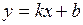 (5)
(5)
называется уравнением прямой с угловым коэффициентом.
 y
y 
 b α
b α
x
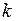 =tgα – угловой коэффициент.
=tgα – угловой коэффициент.
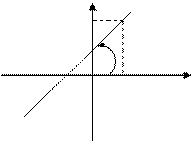
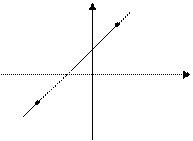
6. Уравнение прямой, проходящей через данную точку в данном направлении.
 y
y 
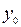
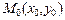
α
0  x
x
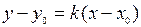 , (6)
, (6)
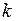 =tgα.
=tgα.
7. Уравнение прямой, проходящей через две данные точки.
 y
y
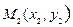
x
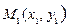
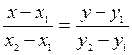 . (7)
. (7)
8. Уравнение прямой в отрезках на осях.
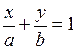 . (8)
. (8)
 y
y
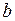
x
0 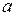
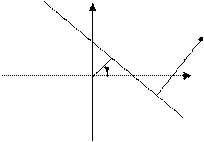
9. Нормальное уравнение прямой линии на плоскости. Расстояние от точки до прямой на плоскости.
 y
y
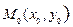
p α x
0 d
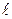
Нормаль к прямой образует угол α с положительным направлением оси 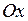 .
.
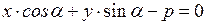 . (9)
. (9)
Расстояние от точки до прямой на плоскости находится по формуле:
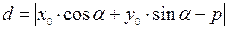 . (10)
. (10)
Для нормального уравнения (9) характерно, что
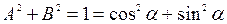 .
.
Чтобы привести общее уравнение прямой к нормальному виду надо обе части этого уравнения умножить на нормирующий множитель 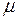 :
:
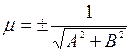 . (11)
. (11)
Знак нормирующего множителя выбирается противоположным знаку свободного члена С в общем уравнении прямой.
10. Параметрические уравнения прямой на плоскости.


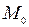

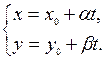
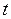 – параметр,
– параметр, 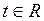 .
.
Пусть две прямые заданы уравнениями:
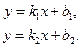
 |
(2) (1)
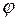
|
Тангенс угла между этими прямыми находится по формуле
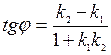 . (12)
. (12)
Признаком параллельности двух прямых является равенство их угловых коэффициентов
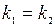 . (13)
. (13)
Признаком перпендикулярности двух прямых является соотношение
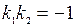 (14)
(14)
или 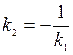 .
.
Угловые коэффициенты взаимно перпендикулярных прямых обратны по величине и противоположны по знаку.
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 451; Нарушение авторских прав?; Мы поможем в написании вашей работы!