
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Генеральная средняя. Выборочная средняя. Оценка генеральной средней по выборочной средней
|
|
|
|
Пусть требуется изучить генеральную совокупность относительно количественного признака X.
Распределение признака и в генеральной, и в выборочной совокупности будем считать дискретными, т.к. от непрерывных распределений всегда можно перейти к дискретным.
Определение. Генеральной средней  называют среднее арифметическое значений признака X генеральной совокупности.
называют среднее арифметическое значений признака X генеральной совокупности.
Если значения 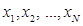 различны, то
различны, то
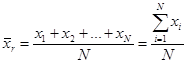 .
.
Поскольку исследуемый признак Xможно рассматривать как случайную величину, возможные значения которой 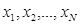 имеют одинаковую вероятность
имеют одинаковую вероятность  (вероятность извлечь объект со значением
(вероятность извлечь объект со значением 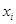 равна
равна 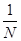 ), то
), то 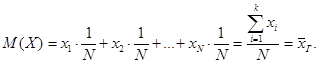
Итак, 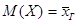 . (1)
. (1)
Если значения  имеют соответственно частоты
имеют соответственно частоты  , причем
, причем  , то
, то

Формула (1) остается справедливой и в этом случае.
Замечание. Все рассуждения были приведены, когда X - дискретная случайная величина.
При непрерывном распределении признака X по определению, полагают 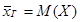 .
.
Для изучения генеральной совокупности относительно признака X извлекается выборка объема n.
Определение. Выборочной средней 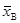 называют среднее арифметическое значений признака выборочной совокупности.
называют среднее арифметическое значений признака выборочной совокупности.
Если 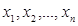 различны, то
различны, то

Если  имеют соответственно частоты
имеют соответственно частоты 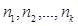 , причем
, причем 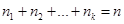 , то
, то
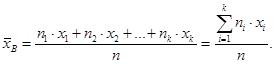 (2)
(2)
Замечание. Выборочная средняя, найденная по данным одной выборки, есть число. Если извлекать из этой генеральной совокупности другие выборки того же объекта, то выборочная средняя будет изменяться от выборки к выборке.
Задача. Пусть из генеральной совокупности извлечена повторная выборка объема n со значениями признака 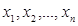 (будем считать их различными). Генеральная средняя
(будем считать их различными). Генеральная средняя  – неизвестна. Требуется оценить
– неизвестна. Требуется оценить  по данным выборки. Выборочную среднюю принимают в качестве оценки генеральной средней.
по данным выборки. Выборочную среднюю принимают в качестве оценки генеральной средней.
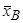 - оценка
- оценка  .
.
Будем рассматривать  как случайную величину
как случайную величину  ;
;  как независимые одинаково распределенные величины
как независимые одинаково распределенные величины 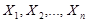 , имеющие то же распределение, что и X.
, имеющие то же распределение, что и X.
1. Докажем, что средняя выборочная – несмещенная оценка генеральной средней, т.е. 
 .
.
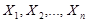 имеют то же распределение, что и X. Обозначим
имеют то же распределение, что и X. Обозначим  , следовательно,
, следовательно, 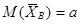 ,
, 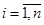 . Тогда
. Тогда

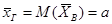 , следовательно,
, следовательно, 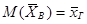 , что и требовалось доказать.
, что и требовалось доказать.
Докажем, что выборочная средняя - состоятельная оценка генеральной средней.
Предположим, что Х1, Х2, …, Хn имеют ограниченные дисперсии. Тогда согласно частному случаю теореме Чебышева:
 или
или 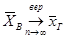 , что и требовалось доказать.
, что и требовалось доказать.
Итак,  - несмещенная состоятельная оценка
- несмещенная состоятельная оценка  .
.
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 9683; Нарушение авторских прав?; Мы поможем в написании вашей работы!