Дифракция Френеля на круглом отверстии и диске

Рассмотрим случай, когда на малое круглое отверстие ра­диусом r падает плоская монохроматическая волна с длиной волны λ. Согласно принципу Гюйгенса-Френеля плоский фронт волны, совпадающий с плоскостью круглого отверстия, можно рассматривать как множество фиктивных источников, испускающих когерентные волны. В точке М, лежащей на оси отверстия, эти волны будут интерферировать (рис. 3).

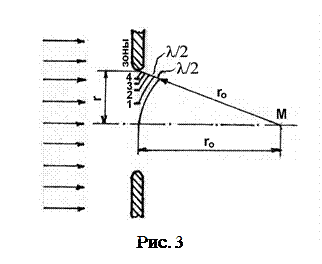Разобьем площадь отверстия на ряд кольцевых зон Френеля. Для этого из точки М последовательно проводятся окружности радиусом 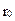; ; 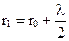; 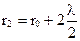- и т.д. Так как лучи, идущие от край­них точек зоны, имеют разность хода в полволны, то колебания от этих двух точек приходят в точку М в противоположной фазе и гасят друг друга. Для каждой точки каждой зоны найдется точка в со­седней зоне с разностью хода в полволны. Поэтому, если число зон, которые укладываются в отверстии, четное, то в точке М будет темное пятно, а если нечетное, то – светлое.

Если отверстие открывается всего лишь на одну зону или небольшое число нечетных зон, то амплитуда колебаний, а значит и интенсивность света в точке М будет больше, чем в случае отсутствия экрана с отверстием. Максимум интенсивности света в точке М соот­ветствует размеру отверстия в одну зону. Число зон Френеля в од­ном и том же отверстии зависит от r₀. Предположим, что радиус ρ_к к-ой зоны равен радиусу отверстия. Тогда

,

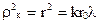откуда число зон Френеля k, укладывающихся на отверстии, будет равно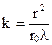

и при λ = const и r = const, будет функцией расстояния r₀, т.е. k = f(r₀).

При перемещении экрана относительно отверстия число зон Фре­неля, укладывающееся на отверстии, будет изменяться (при удале­нии уменьшаться) становясь то четным, то нечетным, а на экране в центре будет то темное, то светлое пятно. Случаю, когда к = 1, со­ответствует 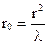. Доказано, что начиная с этого расстояния пучок света становится относительно быстро расширяющимся вследствие дифракции света. Расчет амплитуды колебаний, пришедших в дру­гие точки экрана более сложен. Из соображений симметрии сле­дует, что интерференционная картина на экране вокруг централь­ного светлого или темного пятна должна иметь вид чередующихся светлых и темных колец с центрами в точке М. Если отверстие освеща­ется немонохроматическим светом, то кольца имеют радужную окраску, т.к. число зон Френеля зависит от λ. Случай дифракции на круглом отверстии имеет большое практическое значение, ибо все оправы объективов и линз имеют обычно круглую форму.

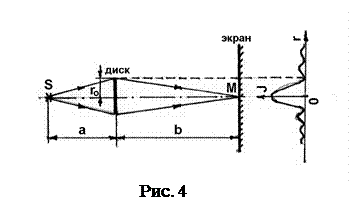
Поместим между точечным источником света s и экраном непрозрачный круглый диск радиусом r₀, так, чтобы он закрыл m первых зон Френеля (рис. 4). Тогда амплитуда световой волны в точке М будет

.

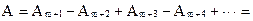
В центре картины при любом (четным или нечетном) m получается светлое пятно. Дифракционная картина в других точках экрана на расстоя­нии r от точки М будет иметь вид чередующихся концентрических светлых и темных колец. Зависимость интенсивности света I от r дана на рис. 4. Если непрозрачный диск закрывает много зон Френеля, чередование светлых и темных колец наблюдается лишь в узкой области на границе геометрической тени. В этом случае А_m+1 «A₁ и интенсивность света в области геометрической тени (за исключением центральной точки) равна нулю. Если диск закрывает лишь небольшую часть первой зоны Френеля, он совсем не отбрасывает тени – освещенность экрана всюду остается такой же, как и при отсутствии преград.

Зависимость между a, b, r_m, m, λ для дифракции на круглом отверстии и на диске дается соотношением

Дата добавления: 2014-01-07