Дифракция на щели

Дифракция Фраунгофера

Пусть на щель АВ шириной а падает плоская монохромати­ческая вол-

на (рис. 5).

В соответствии с принципом Гюйгенса-Френеля освещенную щель можно рассматривать как множество точечных когерентных источников света, так что от каждой точки щели распространяются световые когерентные лучи по всем направлениям. За щелью поместим собирающую линзу, которая собирает лучи в своей фокальной плоскости. В фокальной плоскости поместим экран.

В направлении главной оптической оси линзы, совпадающей с пер­воначальным направлением волны (лучей), линза соберет лучи в своем главном фокусе F. Все эти лучи до точки схождения F про­ходят одинаковые оптические пути, поэтому все эти лучи придут в одинаковой фазе и усилят друг друга. Следовательно, в главном фокусе линзы всегда будет наблюдаться максимум света, который имеет вид ярко освещенной полосы, идущей параллельно щели. Рассмотрим теперь лучи, идущие под углом φ к первоначальному направлению. Эти лучи линза соберет в побочном фокусе Р. Лучи когерентны, поэтому они будут интерферировать. До точки Р лучи, исходящие из разных точек щели, проходят различные пути.

Проведем перпендикуляр АС – новый фронт волны для лу­чей, идущих под углом φ. От этой плоскости АС до точки Р лучи проходят одинаковые оптические пути, тогда как от щели до нее лучи про­ходят разные пути. Между лучами, идущими от крайних точечных источников на щели образуется разность хода ВС, равная δ = a sinφ, где а – ширина щели, равная отрезку АВ.

Воспользуемся методом зон Френеля. На отрезке ВС = δ от­ложим отрезки, равные λ/2, и через эти точки проведем плоскости, параллельные АС. Эти плоскости разделят щель на зоны Френеля, которые в данном случае будут представлять собой полоски, парал­лельные краям щели. Из такого построения ясно, что разность хода лучей, идущих от симметричных точек двух соседних зон Френеля, равна λ/2. На щели укладывается k зон Френеля, равное

.

Если k – четное число (k = 2m), где m = 1, 2, 3, …, то на щели ук­ладывается четное число зон Френеля, которые попарно гасят друг друга. В этом случае в направлении, определяемым углом φ, будут минимумы света. Следовательно, условие минимумов имеет вид:

± где m = 1, 2, …

Если же k – нечетное число (2m +1), то в соответствующих направ­лениях получим максимум света. Следовательно, условие максиму­мов света имеет вид:

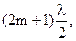± где m = 0, 1, 2, …

При неизменной ширине щели максимумы света различной длины волны приходятся на различные углы. Если щель освещается белым светом, то нулевой (центральный) максимум будет белым. По обе стороны от него расположатся максимумы первого и после­дующего порядков. Они будут цветными, т.к. согласно формуле красный цвет (λ = 0,76 мкм) отклонится на больший угол, чем фио­летовый (λ = 0,38 мкм). Между ними расположатся полосы осталь­ных цветов спектра.

Дата добавления: 2014-01-07