
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Алгоритм построения последовательности
|
|
|
|
1. Выбирается начальная точка 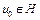 . Общего правила выбора начальной точки не имеется.
. Общего правила выбора начальной точки не имеется.
2. Вычисляется градиент функционала  . Методы вычисления градиента функционала
. Методы вычисления градиента функционала 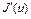 приведены в главе 3.
приведены в главе 3.
3. Следующее приближение 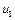 определяется так:
определяется так: 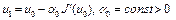 . В общем случае
. В общем случае
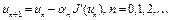 , (2) где
, (2) где 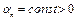 – шаг градиентного метода.
– шаг градиентного метода.
4. Существуют различные способы выбора величины 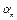 . Ниже приведены некоторые из них:
. Ниже приведены некоторые из них:
а) в методе скорейшего спуска число 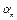 выбирается из условия
выбирается из условия
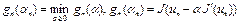 ; (3)
; (3)
б) можно принять  – заданная величина, так, чтобы выполнялось неравенство
– заданная величина, так, чтобы выполнялось неравенство  . Если данное неравенство не выполняется, то дробят число
. Если данное неравенство не выполняется, то дробят число  до тех пор, пока не выполнится данное неравенство (например,
до тех пор, пока не выполнится данное неравенство (например,  и т.д.);
и т.д.);
в) если функционал  , то величину
, то величину 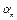 можно выбрать из условий
можно выбрать из условий  , где
, где  – постоянная Липшица из неравенства
– постоянная Липшица из неравенства 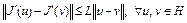 ;
;
г) можно задать последовательность  по алгоритму
по алгоритму 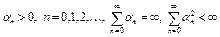 .
.
(например, 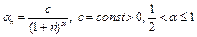 ). Необходимо проверять неравенства
). Необходимо проверять неравенства  .
.
Теорема 1. Пусть функционал 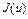 определен в гильбертовом пространстве H, принадлежит классу
определен в гильбертовом пространстве H, принадлежит классу 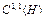 , ограничен снизу, т.е.
, ограничен снизу, т.е. 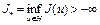 . Пусть последовательность
. Пусть последовательность  построена по алгоритму (2), (3). Тогда:
построена по алгоритму (2), (3). Тогда:
1) числовая последовательность  строго убывает;
строго убывает;
2) 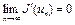 .
.
Доказательство. Из (3) следует, что  . Тогда имеет место неравенство
. Тогда имеет место неравенство  . Отсюда, с учетом того, что
. Отсюда, с учетом того, что 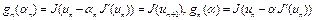 , имеем
, имеем
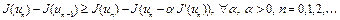 . (4)
. (4)
Поскольку 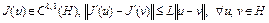 , то, согласно лемме 4 (лекция 2), выполняется неравенство
, то, согласно лемме 4 (лекция 2), выполняется неравенство
 .
.
Следовательно,
 .
.
Из правого неравенства следует, что
 .
.
Отсюда при  имеем
имеем
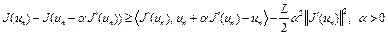 . (5)
. (5)
Теперь неравенство (4) с учетом соотношения (5) запишется в виде
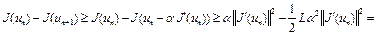
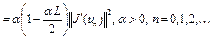 . (6)
. (6)
Из (6) следует, что
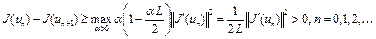 , (7) где максимум достигается при
, (7) где максимум достигается при 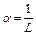 . Если для некоторого конечного n градиент
. Если для некоторого конечного n градиент  , то
, то 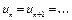 и
и 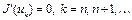 , так что
, так что 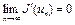 . Представляет интерес случай, когда
. Представляет интерес случай, когда  для конечного n. Поскольку величина
для конечного n. Поскольку величина , то из (7) следует, что числовая последовательность
, то из (7) следует, что числовая последовательность  строго убывает (
строго убывает ( ). Так как функционал
). Так как функционал 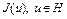 ограничен снизу, то числовая последовательность
ограничен снизу, то числовая последовательность  ограничена снизу. Следовательно, существует предел
ограничена снизу. Следовательно, существует предел  , а из существования предела следует, что
, а из существования предела следует, что 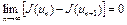 . Переходя к пределу при
. Переходя к пределу при  из (9), имеем
из (9), имеем 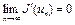 .Теорема доказана.
.Теорема доказана.
Теорема 2. Пусть выполнены условия теоремы 1, и пусть, кроме того:
1) функционал 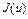 выпуклый на H;
выпуклый на H;
2) множество  ограничено.
ограничено.
Тогда последовательность  минимизирует функционал
минимизирует функционал 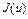 на H и слабо в H сходится к множеству
на H и слабо в H сходится к множеству  , причем справедлива следующая оценка скорости сходимости
, причем справедлива следующая оценка скорости сходимости
 , (8) где
, (8) где 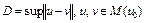 – диаметр множества
– диаметр множества 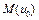 .
.
Доказательство. Покажем, что множество 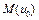 слабо бикомпактно. Поскольку
слабо бикомпактно. Поскольку 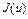 выпуклый функционал, то для любых
выпуклый функционал, то для любых  и при всех
и при всех 
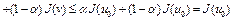 . Следовательно, точка
. Следовательно, точка  . Это означает, что множество
. Это означает, что множество 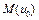 выпукло.
выпукло.
Пусть 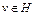 – предельная точка множества
– предельная точка множества 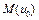 . Тогда существует последовательность
. Тогда существует последовательность  такая, что
такая, что  при
при 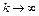 . Так как
. Так как 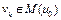 , то
, то 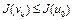 . Тогда в силу того, что
. Тогда в силу того, что 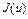 непрерывен в H, имеем
непрерывен в H, имеем 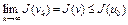 , т.е. точка
, т.е. точка  . Таким образом,
. Таким образом, 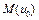 – ограниченное выпуклое замкнутое множество в банаховом пространстве H. Тогда согласно теореме 6 (лекция 10) множество
– ограниченное выпуклое замкнутое множество в банаховом пространстве H. Тогда согласно теореме 6 (лекция 10) множество 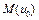 слабо бикомпактно.
слабо бикомпактно.
Выпуклый функционал 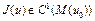 слабо полунепрерывен снизу на
слабо полунепрерывен снизу на 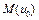 и достигает нижней грани на множестве
и достигает нижней грани на множестве  . Так как
. Так как  , то последовательность
, то последовательность 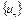 , построенная по алгоритму (2), (3), принадлежит множеству
, построенная по алгоритму (2), (3), принадлежит множеству 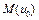 .
.
Покажем, что последовательность 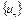 из (2), (3) является минимизирующей, т.е.
из (2), (3) является минимизирующей, т.е.  , где
, где 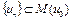 по доказанному выше. В самом деле, так как
по доказанному выше. В самом деле, так как 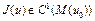 – выпуклый функционал, то согласно теореме 3 (лекция 6) выполняется неравенство
– выпуклый функционал, то согласно теореме 3 (лекция 6) выполняется неравенство  . Тогда
. Тогда 
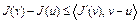 ,
,  . Отсюда, в частности, при
. Отсюда, в частности, при 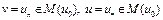 получим
получим
 , (9) где
, (9) где 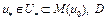 – диаметр множества
– диаметр множества 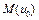 . Переходя к пределу при
. Переходя к пределу при  из (9), с учетом того, что
из (9), с учетом того, что  при
при  , имеем
, имеем
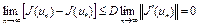 .
.
Тогда  . Следовательно, последовательность
. Следовательно, последовательность 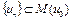 минимизирующая.
минимизирующая.
Поскольку 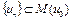 ,
, 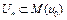 , множество
, множество 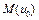 слабо бикомпактно, то последовательность
слабо бикомпактно, то последовательность 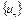 слабо сходится к множеству
слабо сходится к множеству  .
.
Пусть 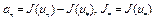 . Тогда неравенства (7), (9) запишутся так
. Тогда неравенства (7), (9) запишутся так
 . (10)
. (10)
Отсюда следует, что последовательность удовлетворяет условиям:
удовлетворяет условиям: 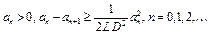 . Верна следующая лемма: если числовая последовательность
. Верна следующая лемма: если числовая последовательность  такая, что
такая, что 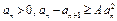 при всех
при всех  , то справедливо неравенство
, то справедливо неравенство  .
.
Применяя данную лемму, из (10) получим (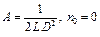 )
)
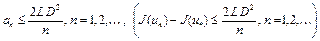 .
.
Итак, доказана оценка (8). Теорема доказана.
Теорема 3. Пусть выполнены условия теоремы 1, и пусть, кроме того, 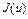 сильно выпуклый функционал на H. Тогда:
сильно выпуклый функционал на H. Тогда:
1) последовательность 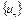 сходится к единственной точке
сходится к единственной точке  ;
;
2) справедливы следующие оценки скорости сходимости
 , (11)
, (11)
 , (12) где
, (12) где  – постоянная сильной выпуклости,
– постоянная сильной выпуклости,  .
.
Доказательство. Свойства сильно выпуклых функционалов приведены в лекции 7. Как следует из теоремы 4 (лекция 7), множество  – выпукло, ограничено и замкнуто, где
– выпукло, ограничено и замкнуто, где 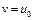 . Множество
. Множество 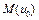 слабо бикомпактно и остаются верными все утверждения теоремы 2. Так как сильно выпуклый функционал является строго выпуклым, то согласно теореме о глобальном минимуме (лекция 8) множество
слабо бикомпактно и остаются верными все утверждения теоремы 2. Так как сильно выпуклый функционал является строго выпуклым, то согласно теореме о глобальном минимуме (лекция 8) множество  содержит единственную точку
содержит единственную точку  .
.
Как следует из теоремы 1 (лекция 7), верно неравенство
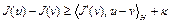
 .
.
Тогда

 .
.
Отсюда при 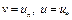 имеем
имеем
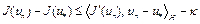

–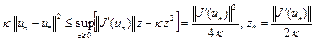 ,
,
где  . Таким образом, величина
. Таким образом, величина
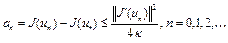 . (13)
. (13)
Как было доказано выше, верно неравенство (см. (10))
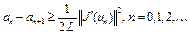 . (14)
. (14)
Из (13), (14) следует, что последовательность  удовлетворяет условиям
удовлетворяет условиям
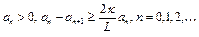 . (15)
. (15)
Как следует из теоремы 2 (лекция 7), верно неравенство
 ,
,  . (16)
. (16)
Так как 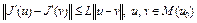 , то
, то
 (17)
(17)
Из (16), (17) следует, что 
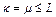 . Тогда
. Тогда  . Из (15) имеем
. Из (15) имеем
 .
.
Отсюда имеем
 .
.
Следовательно, 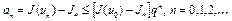 . Оценка (11) доказана.
. Оценка (11) доказана.
Из теоремы 4 (лекция 7) следует, что
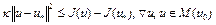 .
.
Отсюда при  , получим
, получим

Тогда 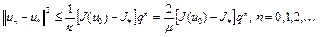 .
.
Теорема доказана.
Пример 1. Рассмотрим задачу оптимального управления (1) – (3) из лекции 11, когда  :
:
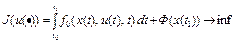 , (18)
, (18)
 , (19)
, (19)
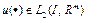 . (20)
. (20)
Как показано в лекциях 11, 12, если выполнены условия теоремы 1 (лекция 11) и теоремы 1 (лекция 12), то функционал 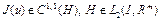 , причем
, причем
 ,
,
где  – решение дифференциального уравнения
– решение дифференциального уравнения
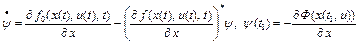 .
.
Последовательность 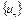 определяется по формуле
определяется по формуле
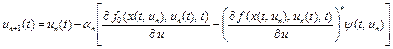 , где
, где  – решение дифференциального уравнения
– решение дифференциального уравнения
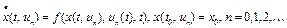 ,
,
а функция  – решение сопряженной системы
– решение сопряженной системы
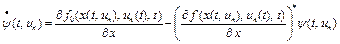 ,
,
 .
.
Величины  определяются из условия
определяются из условия
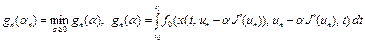 .
.
Для задачи оптимального управления (18) – (20) применима теорема 1. Следовательно, значение функционала (18) при условиях (19), (20) строго убывает и
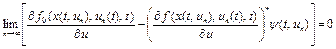 .
.
ЛЕКЦИЯ 17. МЕТОД ПРОЕКЦИИ ГРАДИЕНТА
Рассмотрим оптимизационную задачу
 , (1) где U – выпуклое замкнутое множество гильбертова пространства H,
, (1) где U – выпуклое замкнутое множество гильбертова пространства H, 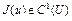 .
.
Алгоритм построения последовательности. 1. Выбирается начальная точка  . 2. Вычислим градиент функционала
. 2. Вычислим градиент функционала  . 3. Определяется точка
. 3. Определяется точка  . 4. Находим проекцию точки
. 4. Находим проекцию точки  на множестве U. В результате находим следующее приближение
на множестве U. В результате находим следующее приближение  . В общем случае
. В общем случае
 , (2) где число
, (2) где число 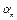 выбирается из условия
выбирается из условия  .
.
5. Существуют различные способы выбора 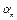 . В частности:
. В частности:
а) если  , то
, то 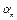 может быть выбрано из условий
может быть выбрано из условий
 . (3)
. (3)
В случае 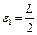 имеем
имеем 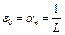 .
.
б) 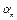 определяется из условия
определяется из условия 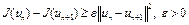 .
.
в)  .
.
Теорема 1. Пусть функционал 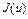 определен на выпуклом замкнутом множестве
определен на выпуклом замкнутом множестве 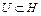 , и пусть, кроме того:
, и пусть, кроме того:
1)  , т.е.
, т.е. 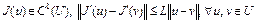 ;
;
2) 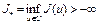 , т.е. функционал ограничен снизу;
, т.е. функционал ограничен снизу;
3) последовательность  определяется по формулам (2), (3). Тогда:
определяется по формулам (2), (3). Тогда:
1. 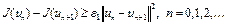 ; (4)
; (4)
2. 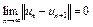 . (5)
. (5)
Доказательство. Поскольку точка  является проекцией
является проекцией  на множество, то согласно теореме 6 (лекция 8) имеем
на множество, то согласно теореме 6 (лекция 8) имеем 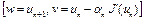
 . (6)
. (6)
Отсюда получим
 . (7)
. (7)
Согласно лемме 4 (лекция 2) справедливо неравенство
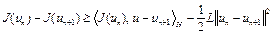 . (8)
. (8)
Из соотношений (7), (8) с учетом неравенства (3) имеем
 , (9)
, (9)
 ,
,
где 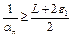 . Из неравенства (9) следует, что числовая последовательность
. Из неравенства (9) следует, что числовая последовательность  строго убывает, из-за ограниченности снизу значения функционала она сходится. Следовательно,
строго убывает, из-за ограниченности снизу значения функционала она сходится. Следовательно, 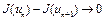 при
при  . Тогда из (9), переходя к пределу при
. Тогда из (9), переходя к пределу при  , имеем
, имеем  при
при  . Теорема доказана.
. Теорема доказана.
Теорема 2. Пусть выполнены условия теоремы 1, и пусть, кроме того, 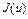 – выпуклый функционал, множество
– выпуклый функционал, множество 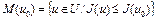 ограничено.
ограничено.
Тогда:
1) последовательность 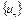 является минимизирующей
является минимизирующей  ;
;
2) последовательность 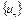 слабо сходится к множеству
слабо сходится к множеству  ;
;
3) справедлива следующая оценка скорости сходимости
 . (10)
. (10)
Доказательство. Как и в доказательстве теоремы градиентного метода, можно показать, что: 1) 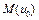 – ограниченное выпуклое замкнутое множество; 2) функционал
– ограниченное выпуклое замкнутое множество; 2) функционал 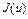 достигает нижней грани на множестве
достигает нижней грани на множестве 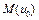 ; 3) последовательность
; 3) последовательность 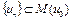 .
.
Покажем, что последовательность 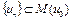 минимизирующая. Поскольку
минимизирующая. Поскольку 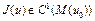 – выпуклый функционал, то
– выпуклый функционал, то
 .
.
Отсюда при  получим
получим

 . (11)
. (11)
Как следует из соотношения (7), справедливо неравенство (при  )
)
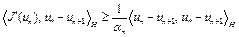 . (12)
. (12)
Тогда из (11), (12) следует, что
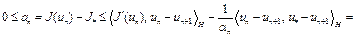
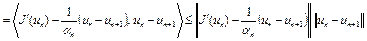 .
.
Отсюда с учетом того, что

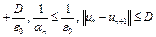 ,
,
где D – диаметр множества 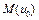 , получим
, получим
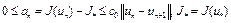 . (13)
. (13)
Так как по доказанному выше (см. (5))  при
при  , то из (13) следует, что
, то из (13) следует, что  . Это означает, что последовательность
. Это означает, что последовательность  является минимизирующей.
является минимизирующей.
Заметим, что 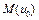 слабо бикомпактное множество,
слабо бикомпактное множество,  , следовательно, все слабо предельные точки
, следовательно, все слабо предельные точки 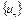 принадлежат множеству
принадлежат множеству 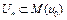 .
.
Из неравенств (9), (13) следует, что
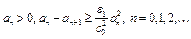 .
.
Отсюда, в силу леммы о числовой последовательности  , получим оценку (10), где
, получим оценку (10), где 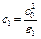 . Теорема доказана.
. Теорема доказана.
Теорема 3. Пусть выполнены условия теоремы 1, и пусть, кроме того, 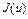 – сильно выпуклый функционал на U. Тогда последовательность
– сильно выпуклый функционал на U. Тогда последовательность  сходится к единственной точке минимума
сходится к единственной точке минимума  , верна оценка
, верна оценка
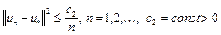 . (14)
. (14)
Доказательство. Поскольку сильно выпуклый функционал является строго выпуклым, то, как следует из теоремы о глобальном минимуме, 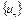 сходится к единственной точке
сходится к единственной точке  ,
,
Как следует из теоремы 4 (лекция 7), верно неравенство
 .
.
Тогда  . Следовательно, верна оценка (14). Теорема доказана.
. Следовательно, верна оценка (14). Теорема доказана.
Пример 1. Рассмотрим задачу оптимального управления
 , (15)
, (15)
 , (16)
, (16)
 , (17) где
, (17) где  – заданные непрерывные функции (см. (1) – (3), лекция 11). Построим последовательность
– заданные непрерывные функции (см. (1) – (3), лекция 11). Построим последовательность  для задачи (15) – (17). Полагаем, что выполнены условия теоремы 1 (лекция 11) и теоремы 1 (лекция 12). Как показано в лекции 17, функционал
для задачи (15) – (17). Полагаем, что выполнены условия теоремы 1 (лекция 11) и теоремы 1 (лекция 12). Как показано в лекции 17, функционал  и в любой точке
и в любой точке  градиент
градиент
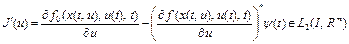 , (18)
, (18)
 . (19)
. (19)
Согласно формуле (2), последовательность  определяется так
определяется так

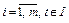 , где
, где 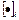 – i-я компонента вектора. (20)
– i-я компонента вектора. (20)
Пример 2. Рассмотрим задачу оптимального управления для линейных систем (см. лекцию 13)
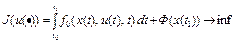 , (21)
, (21)
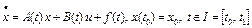 , (22)
, (22)
 . (23)
. (23)
Градиент функционала 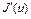 в любой точке
в любой точке  определяется по формуле (см. лекцию 12, формулы (24), (25))
определяется по формуле (см. лекцию 12, формулы (24), (25))
 , (24)
, (24)
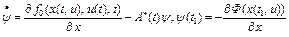 . (25)
. (25)
Последовательность  определяется по формуле (20), где градиент вычисляется по алгоритму (24), (25).
определяется по формуле (20), где градиент вычисляется по алгоритму (24), (25).
Отметим, что: а) если  выпуклые функции, то последовательность
выпуклые функции, то последовательность  является минимизирующей (см. теорему 2); б) если
является минимизирующей (см. теорему 2); б) если  сильно выпуклые функции, то последовательность
сильно выпуклые функции, то последовательность  сходится к единственной точке
сходится к единственной точке  (см. теорему 3).
(см. теорему 3).
Пример 3. Рассмотрим задачу оптимального управления (1) – (4) (лекция 14)
 , (26)
, (26)
 , (27)
, (27)
 , (28)
, (28)
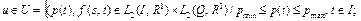
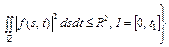 . (29)
. (29)
Градиент функционала 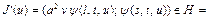
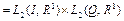 . Тогда последовательность
. Тогда последовательность  строится по алгоритму
строится по алгоритму
 ,
,
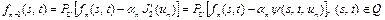 .
.
Согласно результатам лекции 8 (проекция точки на множество) имеем
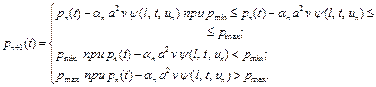 (30)
(30)
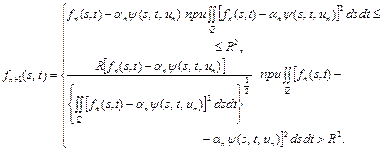 (31)
(31)
Для задачи (26) – (29) последовательности (30) – (31) являются минимизирующими.
Пример 4. Рассмотрим задачу оптимального управления (1) – (5) (лекция 15)
 (32)
(32)
 , (33)
, (33)
 , (34)
, (34)
 , (35)
, (35)
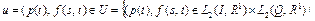
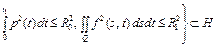 . (36)
. (36)
Градиент функционала (32) при условиях (33) – (36) определяется по формуле 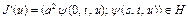 . Последовательность
. Последовательность  строится по алгоритму
строится по алгоритму
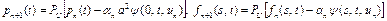 ,
,
 .
.
Тогда
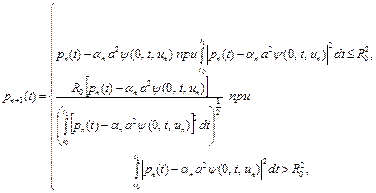 (37)
(37)
 (38)
(38)
Для задачи (32) – (36) последовательности (37), (38) являются минимизирующими.
ЛЕКЦИЯ 18. МЕТОД УСЛОВНОГО ГРАДИЕНТА
Рассмотрим оптимизационную задачу
 , (1) где U – выпуклое замкнутое ограниченное множество из гильбертова пространства H.
, (1) где U – выпуклое замкнутое ограниченное множество из гильбертова пространства H.
Алгоритм построения последовательности. 1. Выбирается начальная точка  . 2. Вычисляется градиент функционала
. 2. Вычисляется градиент функционала  . 3. Определяется вспомогательная точка
. 3. Определяется вспомогательная точка  как решение оптимизационной задачи
как решение оптимизационной задачи
 .
.
4. Следующее приближение 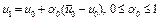 . Поскольку U – выпуклое множество, то
. Поскольку U – выпуклое множество, то  . В общем случае
. В общем случае
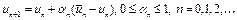 , (2) где
, (2) где 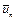 – решение оптимизационной задачи
– решение оптимизационной задачи
 . (3)
. (3)
Поскольку множество U слабо бикомпактно,  – слабо полунепрерывен снизу на U, то точка
– слабо полунепрерывен снизу на U, то точка 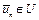 существует (см. лекцию 10).
существует (см. лекцию 10).
5. Существуют различные способы выбора 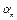 . В частности:
. В частности:
а) 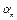 выбирается из условия
выбирается из условия
 ; (4)
; (4)
б) выбрать  и проверить выполнение условия
и проверить выполнение условия  . Если данное условие не выполняется, то необходимо дробить
. Если данное условие не выполняется, то необходимо дробить 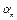 до тех пор, пока не выполняется данное неравенство;
до тех пор, пока не выполняется данное неравенство;
в) если  , то
, то
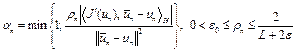 ,
,
 – параметры метода. В частности,
– параметры метода. В частности,  .
.
Теорема 1. Пусть функционал 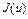 определен на выпуклом ограниченном замкнутом множестве U из гильбертова пространства H, и пусть, кроме того:
определен на выпуклом ограниченном замкнутом множестве U из гильбертова пространства H, и пусть, кроме того:
1)  , т.е.
, т.е.  ;
;
2) последовательность  определяется соотношениями (2) – (4).
определяется соотношениями (2) – (4).
Тогда
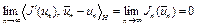 . (5)
. (5)
Доказательство. Покажем, что функционал 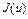 ограничен на множестве U. В самом деле, из включения
ограничен на множестве U. В самом деле, из включения  следует, что (см. лемма 4, лекция 2)
следует, что (см. лемма 4, лекция 2)
 . (6)
. (6)
Отсюда имеем
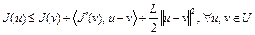 .
.
В частности, при  получим
получим

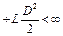 ,
,
где 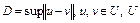 – ограниченное множество. Отсюда следует, что
– ограниченное множество. Отсюда следует, что 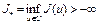 , т.е. функционал
, т.е. функционал 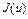 ограничен снизу на U.
ограничен снизу на U.
Из (3) следует, что значение 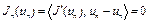 . Тогда
. Тогда 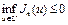 . Так как
. Так как  , то выполняется неравенство
, то выполняется неравенство
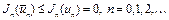 . (7)
. (7)
Поскольку величина 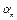 выбирается из условия (4), то
выбирается из условия (4), то 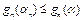 . Отсюда следует, что
. Отсюда следует, что  . Тогда
. Тогда
 . (8)
. (8)
Из (6) имеем
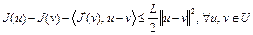 .
.
Тогда
 . (9)
. (9)
Из (8) и (9) при 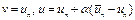 получим
получим

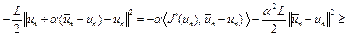
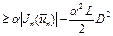 , (10) где
, (10) где 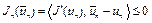 в силу неравенства (7), D – диаметр множества U. Заметим, что если
в силу неравенства (7), D – диаметр множества U. Заметим, что если  , то выполнено неравенство (5) и теорема доказана. Интерес представляет случай, когда
, то выполнено неравенство (5) и теорема доказана. Интерес представляет случай, когда  . Так как
. Так как 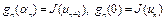 , то из неравенства
, то из неравенства 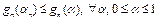 следует, что
следует, что  . Значит, числовая последовательность
. Значит, числовая последовательность  не возрастает. Тогда из ограниченности снизу значения функционала, т.е.
не возрастает. Тогда из ограниченности снизу значения функционала, т.е.  , следует, что числовая последовательность
, следует, что числовая последовательность  сходится. Следовательно,
сходится. Следовательно, 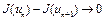 при
при  .
.
Теперь, переходя к пределу при  , из (10) имеем
, из (10) имеем
 .
.
Отсюда при 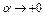 получим
получим
 .
.
Следовательно, 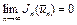 , т.е. верно соотношение (5). Теорема доказана.
, т.е. верно соотношение (5). Теорема доказана.
Теорема 2. Пусть выполнены условия теоремы 1, и пусть, кроме того, 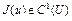 выпуклый функционал. Тогда:
выпуклый функционал. Тогда:
1) последовательность  является минимизирующей, т.е.
является минимизирующей, т.е.  ;
;
2) последовательность 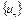 слабо сходится к множеству
слабо сходится к множеству  ;
;
3) справедлива следующая оценка скорости сходимости
 . (11)
. (11)
Доказательство. Поскольку U – слабо бикомпактное множество и выпуклый функционал 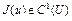 слабо полунепрерывен снизу, то множество
слабо полунепрерывен снизу, то множество  .
.
Покажем, что последовательность  минимизирующая. В этом случае, как в доказательстве предыдущих теорем, справедливо неравенство
минимизирующая. В этом случае, как в доказательстве предыдущих теорем, справедливо неравенство
 ,
,
где  . Отсюда, в силу того, что
. Отсюда, в силу того, что
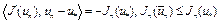 ,
,
получим
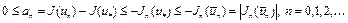 . (12)
. (12)
Отсюда, в силу доказанного  при
при  , имеем
, имеем  . Это означает, что последовательность
. Это означает, что последовательность  минимизирующая.
минимизирующая.
Так как множество U слабо бикомпактно, 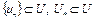 , то минимизирующая последовательность
, то минимизирующая последовательность 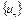 слабо сходится к
слабо сходится к  .
.
Покажем справедливость оценки (11). Поскольку 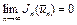 , то найдется номер
, то найдется номер 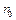 такой, что
такой, что  при всех
при всех  . Как следует из (10),
. Как следует из (10),
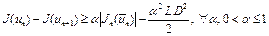 . (13)
. (13)
Заметим, что
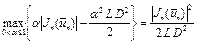 ,
,
где 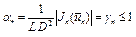 при
при  . Тогда неравенство (13) запишется так
. Тогда неравенство (13) запишется так
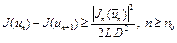 . (14)
. (14)
Из (12), (14) получим
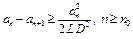 . (15)
. (15)
Далее, применяя лемму о числовой последовательности  (см. лекцию 16), из (15) получим
(см. лекцию 16), из (15) получим
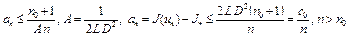 .
.
Отсюда следует оценка (11). Теорема доказана.
Теорема 3. Пусть выполнены условия теоремы 1, и пусть, кроме того, 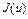 – сильно выпуклый функционал на U. Тогда:
– сильно выпуклый функционал на U. Тогда:
1)последовательность  сходится к единственной точке минимума
сходится к единственной точке минимума  ;
;
2) справедлива следующая оценка скорости сходимости
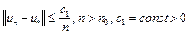 . (16)
. (16)
Доказательство. Как следует из теоремы о глобальном минимуме (см. лекцию 8), в случае, когда 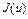 сильно выпуклый функционал, множество
сильно выпуклый функционал, множество  содержит единственную точку минимума. Далее, по доказанному выше, последовательность
содержит единственную точку минимума. Далее, по доказанному выше, последовательность 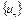 сходится к точке
сходится к точке  .
.
В лекции 7 было доказано, что для сильно выпуклого функционала верно неравенство
 .
.
Отсюда при  имеем
имеем
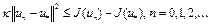 . (17)
. (17)
Из утверждения теоремы 2 следует, что  . Тогда из (17) получим
. Тогда из (17) получим
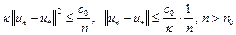 .
.
Отсюда следует оценка (16), где  . Теорема доказана.
. Теорема доказана.
Пример 1. Рассмотрим задачу оптимального управления
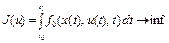 , (18)
, (18)
 , (19)
, (19)
 . (20)
. (20)
Покажем алгоритм решения задачи (18) – (20) методом условного градиента. Заметим, что U – выпуклое ограниченное замкнутое множество из гильбертова пространства  , градиент функционала в точке
, градиент функционала в точке 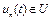 равен
равен
 ,(21)
,(21)
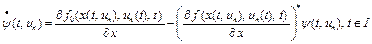 , (22)
, (22)
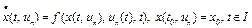 , (23)
, (23)
 . (24)
. (24)
По формулам (21) – (24) можно найти градиент функционала 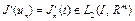 . Итак,
. Итак,  – известная функция.
– известная функция.
Функцию  находим из решения задачи оптимального управления
находим из решения задачи оптимального управления
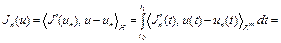
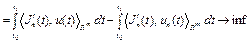 , (25)
, (25)
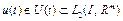 , (26) где
, (26) где 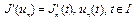 – известные функции,
– известные функции, 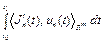 – известное число, минимизируется линейный функционал
– известное число, минимизируется линейный функционал
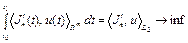 . (27)
. (27)
Из (25) – (27) следует, что компоненты вектор функции 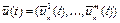 определяются следующим образом
определяются следующим образом

Функция
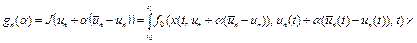
 .
.
Величину 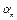 находим из условия
находим из условия  . Следующее приближение
. Следующее приближение 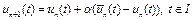 . Аналогичным путем может быть построена последовательность
. Аналогичным путем может быть построена последовательность  для линейной системы.
для линейной системы.
Пример 2. Рассмотрим задачу оптимального управления
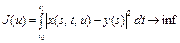 , (28)
, (28)
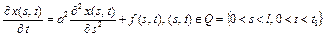 , (29)
, (29)
 , (30)
, (30)

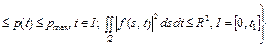 . (31)
. (31)
Для задачи (28) – (31) последовательность 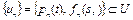 строится по следующему алгоритму, где U – выпуклое ограниченное замкнутое множество из
строится по следующему алгоритму, где U – выпуклое ограниченное замкнутое множество из  , градиент функционала
, градиент функционала
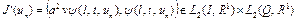 , (32)
, (32)
 , (33)
, (33)
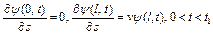 , (34)
, (34)
 , (35)
, (35)
 , (36)
, (36)
 . (37)
. (37)
По формулам (32) – (37) можно найти градиент функционала  . Функцию
. Функцию  находим из решения задачи оптимального управления
находим из решения задачи оптимального управления
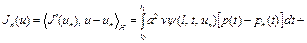
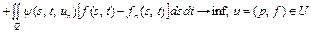 . (38)
. (38)
Решением задачи (38) является
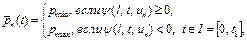 (39)
(39)
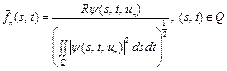 . (40)
. (40)
Величина 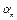 определяется из условия
определяется из условия  , где
, где
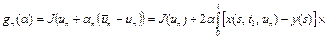
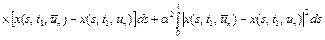 . (41)
. (41)
Из (39) – (41) следует, что  ,
, 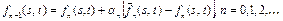 .
.
Последовательность  является минимизирующей в силу того, что функционал
является минимизирующей в силу того, что функционал  выпуклый.
выпуклый.
ЛЕКЦИЯ 19. МЕТОД СОПРЯЖЕННЫХ НАПРАВЛЕНИЙ. МЕТОД НЬЮТОНА
Метод сопряженных направлений. Рассмотрим оптимизационную задачу
 , (1) где H – гильбертово пространство,
, (1) где H – гильбертово пространство,  .
.
Алгоритм построения последовательности. 1. Выбирается начальная точка 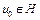 . 2. Вычислим градиент функционала
. 2. Вычислим градиент функционала  . 3. Строится последовательность
. 3. Строится последовательность 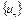 по правилу
по правилу
 , (2) где
, (2) где
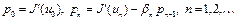 . (3)
. (3)
4. Числовые последовательности 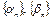 выбираются следующим образом:
выбираются следующим образом:
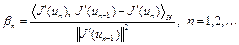 , (4)
, (4)
 . (5)
. (5)
Теорема 1. Пусть функционал 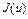 определен на гильбертовом пространстве H, принадлежит классу
определен на гильбертовом пространстве H, принадлежит классу 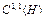 и сильно выпуклый на H, последовательность
и сильно выпуклый на H, последовательность 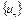 определяется по правилу (2) – (5). Тогда:
определяется по правилу (2) – (5). Тогда:
1) последовательность 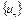 сходится к точке
сходится к точке  ;
;
2) справедливы следующие оценки скорости сходимости
 , (6)
, (6)
 , (7) где
, (7) где  – постоянная Липшица для
– постоянная Липшица для 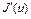 , т.е.
, т.е.  – коэффициент сильной выпуклости.
– коэффициент сильной выпуклости.
Доказательство. Поскольку  – сильно выпуклый функционал, то существует единственная точка
– сильно выпуклый функционал, то существует единственная точка  , где
, где  . Заметим, что функция
. Заметим, что функция  – сильно выпукла по
– сильно выпукла по 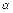 и
и 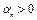 – определяется однозначно. Полагаем, что
– определяется однозначно. Полагаем, что 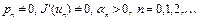 .
.
Из условия (5) следует, что  . Так как
. Так как  , то
, то
 . (8)
. (8)
Можно показать, что
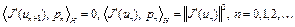 . (9)
. (9)
В самом деле, при 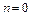 имеем
имеем  , поэтому
, поэтому 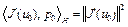 . Из (5) при
. Из (5) при 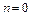 следует, что
следует, что  . Таким образом, равенства (9) при
. Таким образом, равенства (9) при 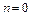 верны. Докажем равенства (9) методом математической индукции. Пусть при
верны. Докажем равенства (9) методом математической индукции. Пусть при 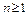 верны равенства
верны равенства  . Тогда
. Тогда 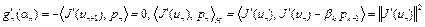 Равенства (9) доказаны.
Равенства (9) доказаны.
Из (8), (9), имеем
 . (10)
. (10)
Так как функционал  сильно выпуклый, то (см. лекцию 7)
сильно выпуклый, то (см. лекцию 7)
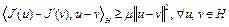 .
.
Отсюда при  имеем
имеем
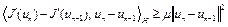 .
.
Тогда с учетом того, что 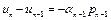 , получим
, получим
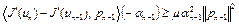 .
.
Отсюда с учетом равенства (9) имеем
 . (11)
. (11)
Из (4) следует, что

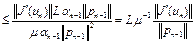
в силу неравенства (11). Отсюда имеем
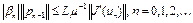 . (12)
. (12)
Так как 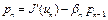 , то
, то
 , (13) в силу равенств (9). Из (12) и (13) следует, что
, (13) в силу равенств (9). Из (12) и (13) следует, что
 . (14)
. (14)
Докажем оценки (6), (7). Из (10), (14) следует, что
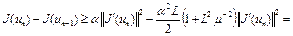
 ,
,
где  .
.
Тогда
 , (15) где
, (15) где  . Как следует из теоремы 1 (лекция 7),
. Как следует из теоремы 1 (лекция 7),
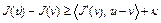
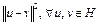 .
.
Тогда

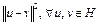 .
.
Отсюда при  имеем
имеем

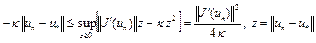 .
.
Следовательно,
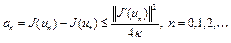 . (16)
. (16)
Из (15), (16) следует, что
 , (17) где
, (17) где 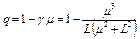 .
.
Из (17) следует, что
 .
.
Следовательно,  , т.е. верна оценка (6). Из теоремы 4 (лекция 7) следует, что
, т.е. верна оценка (6). Из теоремы 4 (лекция 7) следует, что
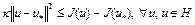 .
.
Отсюда при