Лекция №12. Приложение прецизионных методов измерений

Приложение прецизионных методов измерений

Одним из достаточно широко распространенных приложений прецизионных измерений межплоскостных расстояний является определение остаточных макроскопических упругих напряжений. Остаточные упругие напряжения уравновешиваются в пределах областей существенно больших чем рассеивающий объем. Поэтому можно говорить об однородной деформации решетки, приводящей к сдвигу дифракционных максимумов, что и является основой определения упругих деформаций и вызывающих их напряжений.

Возможности рентгеноанализа упругих напряжений рассмотрим на примере упруго изотропной поликристаллической среды.

Выберем систему координат, показанную на рис. 5, оси координат совпадают с главными осями тензора деформации. В указанной системе координат деформация и напряжение в произвольном направлении ε_φ,ψ и σ_φ,ψ задаются уравнениями:

,

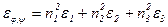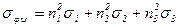
где n_i - направляющие косинусы выбранного направления, определяемого углами φ и ψ;

- главные деформации (d, d₀ - межплоскостные расстояния в деформированной и недеформированной решетках); σ_i - главные напряжения.

В сферических координатах направляющие косинусы выражаются через углы (φ и ψ: n₁ = sinψcosφ, n₂ = sinψsinφ, n₃ = cosψ. Выражение для главных деформаций имеют вид:

,

,

,

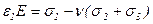где Е, ν - модуль Юнга и коэффициент Пуассона. Теперь выражение для ε_φ,ψ имеет вид:

В формировании дифракционной картины принимает участие лишь тонкий поверхностный слой, толщиной порядка ½μ (μ - коэффициент ослабления рентгеновских лучей). Так как напряжение, действующее нормально к свободной поверхности равно нулю, то это можно отнести и к тонкому поверхностному слою. Следовательно,

,

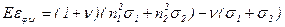Дата добавления: 2014-01-07