Лекция 12. При измерении напряжений неизвестными в двумерной задаче являются напряжения σ1 и σ2, угол φ

Или

,

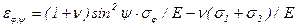где

.

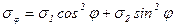При измерении напряжений неизвестными в двумерной задаче являются напряжения σ₁ и σ₂, угол φ, определяющий направление главных осей по отношению к плоскости. 0σ_φε₃ и d₀ - межплоскостное расстояние, отвечающее ненапряженной решетке. Для нахождения этих неизвестных нужно 4 уравнения.

Первое можно получить, измерив межплоскостное расстояние при симметричном отражении от плоскостей, параллельных поверхности (ψ = 0), определяемое суммой главных напряжений:

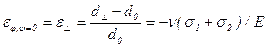
Наклоняя образец (изменяя ψ) при постоянном значении φ т.е. без вращения вокруг нормали к поверхности (ось ε₃), по наклону прямой, изображающей зависимость 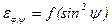найдем:

.

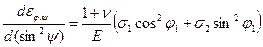Это дает второе уравнение. Повернув образец вокруг оси ε₃ на угол α, получим опять:

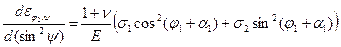
Повернув образец на угол - α, получим, наконец, четвертое уравнение.

Тем самым, если измерять значения , и 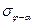можно найти все неизвестные.

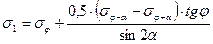
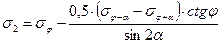
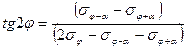
Значения α должны лежать в интервале 0 < α < π/2. Если значение d₀ известно заранее, то достаточно лишь трех уравнений. Проводя измерения в разных точках образца, можно построить распределение напряжений.

Возможности определения упругих напряжений в монокристаллах проиллюстрируем на простейшем примере кристалла кубической сингонии Закон Гука запишется в виде

,

(где ε_ij, σ_kl, s_ijkl - симметричные тензоры деформаций, напряжений и упругой податливости) или в матричной записи:

.

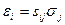Соответственно, для деформации в произвольном направлении :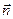

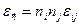, (i, j = 1, 2, 3).

Для отражающего поверхностного слоя компоненты тензора напряжений σ_ij, перпендикулярные поверхности, равны нулю: σ_i3 = 0 (i = 1, 2, 3). (Система координат располагается так, что оси x₁, x₂ расположены в плоскости поверхности, x₃ - нормально поверхности). Итак, имеем систему:

1) 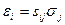(i, j = 1, 2,…,6)

2) 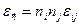(i, j = 1, 2, 3)

3) (i = 1, 2, 3)

Первое уравнение записано в матричной форме, второе и третье -в тензорной. Напомним, что

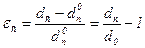
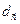(- межплоскостное расстояние для плоскостей, перпендикулярных направлению ).

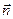Полагая, что при упругой деформации сохраняется квадратичная форма кубической структуры 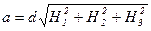, выражение для 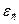записывается в виде:

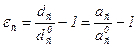
где - период решетки, вычисленный по измеренному 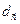; а⁰ - параметр решетки ненапряженного кристалла.

Пусть поверхность кристалла совпадает с плоскостью (001) и система координат с осями [001], [010] и [001]. Выбрав 4 отражения с разными индексами с углами дифракции θ_Б > 60°, найдем компоненты тензора σ_ij (σ₁₁, σ₁₂ и σ₂₂) и а ₀, используя систему (). Так для арсенида галлия и Сu K α₁ -излучения эти отражения: 117, , 155 и .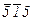

Итак, имеем четыре уравнения и находим неизвестные ,,и .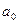

Перейдя к цилиндрическим координатам получим:

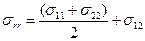
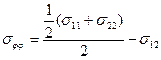
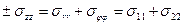
Проведя измерения в нескольких точках сечения кристалла, получим распределение напряжений в сечении (рис. 6). При иной ориентации поверхности необходимо выбрать подходящий ортогональный базис и привести тензор s_ijkl к новой системе координат:

,

где α _ij - компоненты матрицы направляющих косинусов углов между новыми и старыми осями. Затем найдем компоненты тензора σ_ij в новых осях, выбрав подходящие для новой ориентировки отражения. Например для GaAs и ориентировки (111) это: 444, 155, 515, 117.

Автоматизация приёмистости ГТД (продолжение)

Дата добавления: 2014-01-07