
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Метод лексикографического перебора
|
|
|
|
Метод основан на процедуре перебора отдельных точек области возможных решений, аналогичной упорядочению слов в словаре и называемой, поэтому лексикографической.
Все переменные исходной задачи упорядочиваются по быстроте изменения. Если никаких дополнительных соображений при этом не использовать, то этот порядок будет соответствовать естественному порядку нумерации переменных исходной формализованной записи оптимизационной задачи: самой медленноменяющейся переменной будет x[1], а самой быстроменяющейся - x[n].
В процессе перебора каждая переменная принимает последовательно значения 0 и 1. Уменьшение объема вычислений обеспечивается применением фильтрующего ограничения. Фильтрующее ограничение первый раз возникает как только находится план задачи  , считаем на нем значение целевой функции
, считаем на нем значение целевой функции 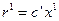 и в дальнейшем рассматриваются только те наборы, которые удовлетворяют фильтрующему ограничению
и в дальнейшем рассматриваются только те наборы, которые удовлетворяют фильтрующему ограничению  . Если дальше находится план с лучшим значением целевой функции, то его используют для построения фильтрующего ограничения. Поскольку чем более жесткие ограничения тем меньше перебор, то самой быстроменяющейся переменной лучше взять переменную с наибольшим коэффициентом линейной целевой функции. С этой же целью первыми лучше проверять более жесткие ограничения, те которым не удовлетворяют большее число вариантов.
. Если дальше находится план с лучшим значением целевой функции, то его используют для построения фильтрующего ограничения. Поскольку чем более жесткие ограничения тем меньше перебор, то самой быстроменяющейся переменной лучше взять переменную с наибольшим коэффициентом линейной целевой функции. С этой же целью первыми лучше проверять более жесткие ограничения, те которым не удовлетворяют большее число вариантов.
Когда все ограничения выполнены, то решением будет последний план, который определял фильтр.
Замечание1. Метод записан для задачи 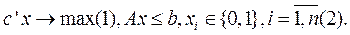 С очевидными изменениями метод применим для задачи на минимум.
С очевидными изменениями метод применим для задачи на минимум.
Замечание 2 Метод применим не только для задач с булевыми переменными, но и для более общих целочисленных задач. При этом значения переменных меняются от заданного  до заданного
до заданного 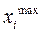 .
.
|
|
|
Дата добавления: 2014-01-07; Просмотров: 747; Нарушение авторских прав?; Мы поможем в написании вашей работы!