Метод направленного частичного перебора по векторной решетке

Опр1. Векторной решеткой называют матаметическую структуру, определяющую расположение и взаимосвязь различных точек целочисленного n –мерного вектора 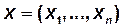, каждая компонента которого может принимать значения от 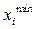до заданного , 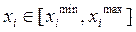. Отдельные точки располагаются по уровням Хемминга, которое определяется через расстояние Хемминга.

Опр2 Расстоянием Хемминга между двумя точками 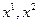называется величина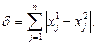

Опр3 Уровнем Хемминга называется местоположение точек векторной решетки, расстояние Хемминга от которых до т.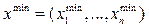одно и то же. При этом номер уровня равен величине расстояния Хемминга.

Как правило, предполагается, что все =0. В этом случае нулевая точка располагается на нулевом уровне, точки (1,0,...,0), (0,1,0,...,0),...,(0,...,0,1) - на первом уровне и т.д.

Опр4 Точки, находящиеся на соседних уровнях и отстоящие друг от друга на расстояние Хемминга равное 1, соединяются дугой.

Пример. Изобразим векторную решетку для случая n=3,

.

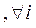
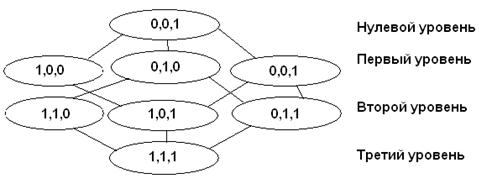
Для решения задачи булевого программирования методом направленного частичного перебора по векторной решетке необходимо, чтобы задача была представлена в форме:

1. Целевая функция на минимум

2. Все коэффициенты целевой функции неотрицательны

3. все ограничения имеют знак (или ):

,

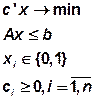Если в исходной задаче некоторый ее коэффициент при j -й переменной C[j]< 0, тo для обеспечения требования 1. в целевой функции и во всех ограничениях необходимо сделать следующую замену переменных

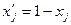
При такой замене,

- во-первых, 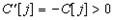(т.е. достигается основная цель замены);

- во-вторых, задача остается комбинаторной {=0, если х[j] = 1; = 1, если x[j]= 0);

- в-третьих, образующаяся при такой замене константа из целевой функции может быть удалена, так как она не оказывает влияния на результат оптимизации.

Дата добавления: 2014-01-07