I. Механика и элементы специальной теории относительности

Омск 2007

МЕХАНИКА, МОЛЕКУЛЯРНАЯ ФИЗИКА И ТЕРМОДИНАМИКА

Циклические формы

Симфония

Фуга

Вариации

Рондо-соната

Рондо

Соната

Концентрическая форма

Концентрическая форма состоит из трёх и более частей, повторяющихся после центральной в обратном порядке, к примеру: А В С В А

Классические формы

Сонатная форма - это форма, в экспозиции (1 часть) которой проводятся две контрастные темы в разных тональностях (главная партия и побочная), которые повторяются в репризе (3 часть) в ином тональном соотношении - тонально сближаясь (чаще всего, обе в тональности главной темы). Срединный раздел (2 часть) представляет собой в типичном случае "Разработку", т.е. тонально неустойчивую часть, где происходит развитие предыдущих интонаций. Сонатная форма выделяется среди всех остальных форм: единственная форма, которая не получила развития в танцевальных и вокальных жанрах.

Свобода, свойственная сонатной форме, расширяется в рондо. Её форма представляет собой конструкцию ABACADAEAF... То есть совершенно разные фрагменты, тональности и размеры связываются начальной темой A.

Произведение, объединяющее несколько разных музыкальных форм, обычно в оркестровом исполнении. Как правило, состоит из четырёх частей (но не обязательно, главная идея симфонии — сочетание разных музыкальных форм):

1. Соната аллегро (быстрая соната).

2. Медленная часть.

3. Менуэт (короткое величественное танцевальное произведение в размере 3/4).

4. Сочетание сонаты и рондо, которое является тематическим повторением первой части.

Крупные произведения, состоящие из отдельных частей, объединенных общим замыслом, относятся к циклическим формам. Части циклических произведений строятся в какой-либо из вышеуказанных форм.

· Сюита

· Сонатно-симфонический цикл

· Концерт — произведение для солирующего инструмента с оркестром.

· Дуэт

· Этюд — краткое произведение, построенное на определённом техническом аспекте, таком как, например, гаммы, и предназначенное для упражнений в исполнительском мастерстве.

· Фантазия — свободная форма.

Конспект лекций для 1 семестра изучения курса «Физика»

1. Кинематика поступательного и вращательного движений

материальной точки

Механическим движением тел называют изменение их положения (или положения их частей) в пространстве с течением времени. В основе классической механики лежат законы Ньютона.

Кинематика изучает механическое движение с геометрической точки зрения и не рассматривает причины, вызывающие это движение. В механике рассматривается движение таких объектов, как материальная точка и абсолютно твердое тело.

Материальной точкой называется тело, размерами которого в данных условиях можно пренебречь.

Абсолютно твёрдым телом называется тело, деформацией которого в данных условиях можно пренебречь. Абсолютно твёрдое тело можно рассматривать как систему материальных точек, жестко связанных между собой.

1.1. Кинематические характеристики движения материальной точки

Описать движение материальной точки – значит знать ее положение относительно выбранной системы отсчета в любой момент времени. Системойотсчёта называется система координат, связанная с телом отсчёта и снабжённая синхронизированными часами. Наиболее часто используется прямоугольная декартова система координат (рис. 1).

Рис. 1

Положение материальной точки характеризуется радиусом-вектором 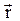, проведённым из начала координат в данную точку (рис. 1). Проекции радиуса-вектора на координатные оси соответствуют координатам точки в выбранной системе координат (рис. 1): 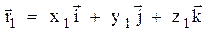  .   Движение материальной точки задано, если известна зависимость координат точки от времени, т.е.

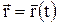или .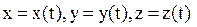

Данные уравнения являются кинематическими уравнениями движения материальной точки, или законом движения точки. В процессе движения конец радиуса-вектора, связанный с точкой, описывает в пространстве кривую, называемую траекторией движения материальной точки. В зависимости от формы траектории различают прямолинейное и криволинейное движения.

Перемещением материальной точки назы­ва­ют вектор, проведённый из начальной точки в конечную точку траектории (рис. 1):

.

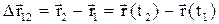Вектор 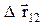может быть выражен через приращения координат и орты соответствующих осей (единичные векторы, направленные по осям):

.

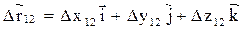Модуль вектора перемещения можно определить следующим образом:

.

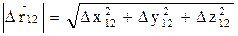Путь материальной точки S₁₂ - это длина траектории.

Скорость - векторная физическая величина, характеризующая быстроту изменения положения тела в пространстве, равная перемещению тела за единицу времени. Различают среднюю и мгновенную скорости.

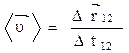- средняя скорость;

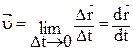- мгновенная скорость;

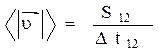- среднее значение модуля скорости.

Вектор средней скорости направлен так же, как и вектор перемещения 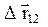. Вектор мгновенной скорости направлен по касательной к траектории движения так же, как вектор элементарного перемещения: . Так как 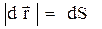, где dS - элементарный путь, то модуль мгновенной скорости равен производной пути по времени:

.

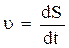В декартовой системе координат скорость можно представить через её проекции на оси:

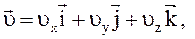
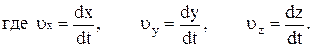
Модуль скорости может быть найден по следующей формуле:

.

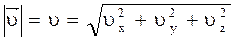При рассмотрении движения тела относительно двух различных инерциальных систем отсчета используют классический закон сложения скоростей: скорость тела относительно неподвижной системы отсчета 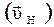равна векторной сумме скорости тела относительно движущейся системы 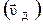и скорости самой движущейся системы относительно неподвижной :

.

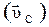Ускорение - векторная физическая величина, характеризующая быстроту изменения скорости с течением времени, равная приращению скорости за единицу времени. Различают среднее и мгновенное ускорения.

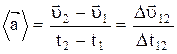- среднее ускорение,

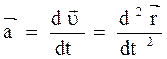- мгновенное ускорение.

Вектор ускорения может быть представлен через его проекции на координатные оси:

,

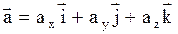где , , .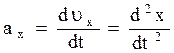

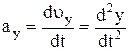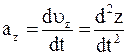Модуль ускорения можно определить следующим образом:

.

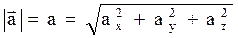1.2. Тангенциальная и нормальная составляющие ускорения

Часто используется представление ускорения через две составляющие: тангенциальное и нормальное ускорения (рис. 2):

Рис. 2

  ;   .  

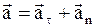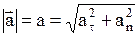Тангенциальное ускорение характеризует изменение скорости по модулю (величине) и направлено по касательной к траектории:

,

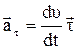где 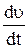- производная модуля скорости, 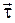- единичный вектор касательной, совпадающий по направлению со скоростью.

Нормальное ускорение характеризует изменение скорости по направлению и направлено по радиусу кривизны к центру кривизны траектории в данной точке:

,

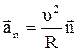где R - радиус кривизны траектории, 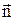- единичный вектор нормали.

Модуль вектора ускорения может быть найден по формуле

.

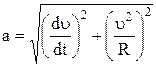1.3. Основная задача кинематики

Основная задача кинематики заключается в нахождении закона движения материальной точки. Для этого используются следующие соотношения:

; ; ; ;

.

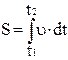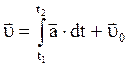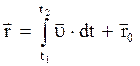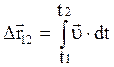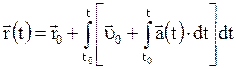Частные случаи прямолинейного движения:

1) равномерное прямолинейное движение: ;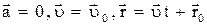

2) равнопеременное прямолинейное движение: .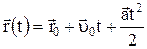

1.4. Вращательное движение и его кинематические характеристики

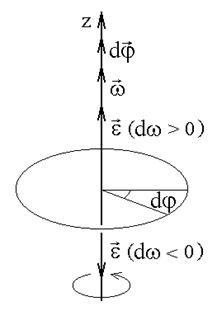
При вращательном движении все точки тела движутся по окружностям, центры которых лежат на одной и той же прямой, называемой осью вращения. Для характеристики вращательного движения вводятся следующие кинематические характеристики (рис. 3).

Угловое перемещение 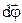- вектор, численно равный углу поворота тела 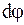за время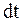и направленный вдоль оси вращения так, что, глядя вдоль него, поворот тела наблюдается происходящим по часовой стрелке.

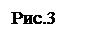
Угловая скорость 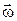- характеризует быстроту и направление вращения тела, равна производной угла поворота по времени и направлена вдоль оси вращения как угловое перемещение.

При вращательном движении справедливы следующие формулы:

; ; .

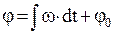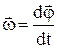Угловое ускорение 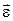характеризует быстроту изменения угловой скорости с течением времени, равно первой производной угловой скорости и направлено вдоль оси вращения:

; ; .

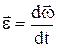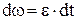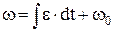Зависимость выражает закон вращения тела.

При равномерном вращении: e = 0, w = const, j = wt.

При равнопеременном вращении: e = const, , .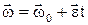

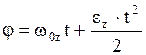Рис. 3

Для характеристики равномерного вращательного движения используются период вращения и частота вращения.

Период вращения Т – время одного оборота тела, вращающегося с постоянной угловой скоростью.

Частота вращения n – количество оборотов, совершаемых телом за единицу времени.

Угловая скорость может быть выражена следующим образом:

.

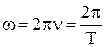Связь между угловыми и линейными кинематическими характеристиками (рис. 4):

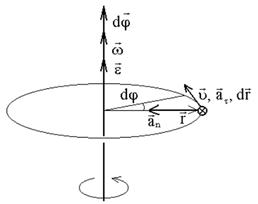
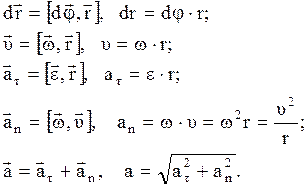
Рис. 4

Дата добавления: 2014-01-07