Алгоритмы и программы

Лекция №1_2

Понятие алгоритма. Понятие алгоритма является одним из основных понятий современной математики. Еще на самых ранних ступенях развития математики (Древний Египет, Вавилон, Греция) в ней ста­ли возникать различные вычислительные процессы чисто механического характера. С их помощью искомые величины ряда задач вычислялись последовательно из исходных величин по определенным правилам и инструкциям. Со временем все такие процессы в математике получили название алгоритмов. Термин алгоритм происходит от имени средневекового узбекского математика Аль-Хорезми, который еще в IX в. (825) дал правила выполнения четырех арифметических действий в десятичной системе счисления. Процесс выполнения арифметических действий был назван алгоризмом. С 1747 г. вместо слова алгоризм стали употреблять алгорисмус, смысл которого состоял в комбинировании четырех операций арифме­тического исчисления — сложения, вычитания, умножения, деления. К 1950 г. алгорисмус стал алгоритмом. Смысл алгоритма чаще всего связывался с алгоритмами Евклида — процессами нахождения наибольшего общего делителя двух натуральных чисел, наибольшей общей меры двух отрезков и т.п.

Под алгоритмом понимали конечную последовательность точно сформулированных правил, которые позволяют решать те или иные классы задач. Такое определение алгоритма не является строго матема­тическим, так как в нем не содержится точной характеристики того, что следует понимать под классом задач и под правилами их решения.

Первоначально для записи алгоритмов пользовались средствами обычного языка (словесное представление алгоритмов). Уточним понятие словесного представления алгоритма на примере нахождения произведения п натуральных чисел — факториал числа п (с = n!), т.е. вычисления по формуле с = 1*2*3*4*...*n. Этот процесс может быть записан в виде следующей системы последовательных указаний (пунктов):

1. Полагаем с равным единице и переходим к следующему пункту.

2. Полагаем i равным единице и переходим к следующему пункту.

3. Полагаем с = i* с и переходим к следующему пункту.

4. Проверяем, равно ли i числу п. Если i = п, то вычисления пре­кращаем. Если i < п, то увеличиваем на единицу и переходим к пункту 3.

В первом алгоритме в качестве элементарных операций используются простейшие арифметические операции умножения, которые могли бы быть разложены на еще более элементарные операции. Мы такого разбиения не делаем в силу простоты и привычности, арифметических правил.

Алгоритмы, в соответствии с которыми решение поставленных задач сводится к арифметическим действиям, называются численными алгоритмами.

Алгоритмы, в соответствии с которыми решение поставленных задач сводится к логическим действиям, называются логическими алгоритмами. Примерами логических алгоритмов могут служить алгоритмы поиска минимального числа, поиска пути на графе, поиска пути в лабиринте и др.

Алгоритмом, таким образом, называется система четких однозначных указаний, которая определяет последовательность действий над некоторыми объектами и после конечного числа шагов приводит к по­лучению требуемого результата.

Свойства алгоритмов. Каждое указание алгоритма предписывает исполнителю выполнить одно конкретное законченное действие. Исполнитель не может перейти к выполнению следующей операции, не закончив полностью выполнения предыдущей. Предписания алгоритма надо выполнять последовательно одно за другим, в соответствии с ука­занным порядком их записи. Выполнение всех предписаний гарантирует правильное решение задачи. Поочередное выполнение команд алгоритма за конечное число шагов приводит к решению задачи, к достижению цели. Разделение выполнения решения задачи на отдельные операции (выполняемые исполнителем по определенным командам) — важное свойство алгоритмов, называемое дискретностью.

Анализ примеров различных алгоритмов показывает, что запись алгоритма распадается на отдельные указания исполнителю выполнить некоторое законченное действие. Каждое такое указание называется командой. Команды алгоритма выполняются одна за другой. После каждого шага исполнения алгоритма точно известно, какая команда должна выполняться следующей. Алгоритм представляет собой последовательность команд (также инструкций, директив), определяющих действия исполнителя (субъекта или управляемого объекта). Таким образом, выполняя алгоритм, исполнитель может не вникать в смысл того, что он делает, и вместе с тем получать нужный результат. В этом случае говорят, что исполнитель действует формально, т.е. отвлекается от содержания поставленной задачи и только строго выполняет некоторые правила, инструкции. Это очень важная особенность алгоритмов. Наличие алгоритма формализовало процесс, исключило рассуждения. Если обратиться к другим примерам алгоритмов, то можно увидеть, что и они позволяют исполнителю действовать формально. Таким образом, создание алгоритма дает возможность решать задачу формально, механически испол­няя команды алгоритма в указанной последовательности.

Построение алгоритма для решения задачи из какой-либо области требует от человека глубоких знаний в этой области, бывает связано с тщательным анализом поставленной задачи, сложными, иногда очень громоздкими рассуждениями. На поиски алгоритма решения некоторых задач ученые затрачивают многие годы. Но когда алгоритм создан, решение задачи по готовому алгоритму уже не требует каких-либо рассуждений и сводится только к строгому выполнению команд алгоритма. Всякий алгоритм составляется в расчете на конкретного исполни­теля и с учетом его возможностей. Для того чтобы алгоритм мог быть выполнен, нельзя включать в него команды, которые исполнитель не в состоянии выполнить. У каждого исполнителя имеется свой перечень команд, которые он может исполнить. Совокупность команд, которые могут быть выполнены исполнителем, называется системой команд исполнителя. Каждая команда алгоритма должна определять однозначно действие исполнителя. Такое свойство алгоритмов называется определенностью (или точностью) алгоритма.

Алгоритм, составленный для конкретного исполнителя, должен включать только те команды, которые входят в его систему команд. Это свойство алгоритма называется понятностью. Алгоритм не должен быть рассчитан на принятие каких-либо самостоятельных решений исполнителем, не предусмотренных составленным алгоритмом.

Еще одно важное требование, предъявляемое к алгоритмам, — результативность (или конечность) алгоритма. Оно означает, что исполнение алгоритма должно закончиться за конечное число шагов.

Разработка алгоритмов — процесс творческий, требующий умственных усилий и затрат времени. Поэтому предпочтительно разрабатывать алгоритмы, обеспечивающие решения всего класса задач данного типа. Например, если составляется алгоритм решения кубического уравнения ах³ + bх^г + сх + d = 0, то он должен быть вариативен, т.е. обеспечивать возможность решения для любых допустимых исходных значений коэффициентов а, b, с, d. Про такой алгоритм говорят, что он удовлетворяет требованию массовости. Свойство массовости не является необходимым свойством алгоритма. Оно скорее определяет качест­во алгоритма; в то же время свойства дискретности, точности, понятно­сти и конечности являются необходимыми (иначе это не алгоритм).

Формы записи алгоритмов. Алгоритмы можно записывать по-разному. Форма записи, состав и количество операций алгоритма зависят от того, кто будет исполнителем этого алгоритма. Если задача решается с помощью ЭВМ, алгоритм решения задачи должен быть записан в понятной для машины форме, т. е. в виде программы. Всякий алгоритм может быть:

-записан на естественном языке (примеры записи алгоритма на ес­
тественном языке приведены при определении понятия алгоритма);

-изображен в виде блок-схемы;

-записан на алгоритмическом языке.

Запись алгоритмов в виде блок-схем. Схема алгоритма — графическое представление алгоритма. Каждый пункт алгоритма отображает­ся на схеме некоторой геометрической фигурой — блоком — и дополняется элементами словесной записи. Правила выполнения схем алгоритмов регламентирует ГОСТ 19.002—80 (единая система программной документации, см. табл. 1.1)

Блоки на схемах соединяются линиями потоков информации. Основное направление потока информации идет сверху вниз и слева на­право (стрелки могут не указываться), снизу вверх и справа налево — стрелка обязательна. Количество входящих линий для блока не ограничено. Выходящая линия должна быть одна (исключение составляет логический блок).

Таблица 1.1. Основные элементы блок-схем

№ п/п	Символ	Наименование	Содержание
1.		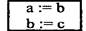Блок вычислений	Вычислительные действия или последовательность действий
2.		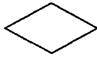Логический блок	Выбор направления выполнения алгоритма в зависимости от некоторого условия
3.		Блоки ввода-вывода данных	1. Общие обозначения ввода (вывода) данных (вне зависимости от физического носителя) 2. Вывод данных, носителем которых является документ
4.		Начало (конец)	Начало или конец алгоритма, вход или выход в программу
5.		Процесс пользователя (подпрограм­ма)	Вычисление по стандартной программе или подпрограмме
6.		Блок модификации	Функция выполняет действия, изменяющие пункты (например, заголовок цикла) алгоритма
7.		Соединитель	Указание связи прерванными линиями между потоками информации в пределах од­ного листа.
8.		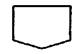Межстраничные соединения	Указание связи между ин­формацией на разных листах

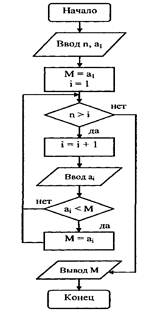
Рис. 1. Блок-схема алгоритма нахождения минимума в последовательности чисел

Приведем запись алгоритма нахождения минимального числа М в последовательности из п чисел a₁, а₂,..., а_п (п ¹ 0) в виде блок-схемы (рис. 1).

Базовые структуры алгоритмов — это определенный набор блоков и стандартных способов их соединения для выполнения типичных последовательностей действий. К основным структурам относятся следующие: линейные (рис. 2, а), разветвляющиеся (рис. 2, б), циклические (рис. 2, в, г).

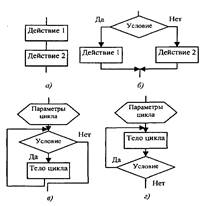
Рис. 2. Базовые структуры алгоритмов и программ

Линейными называются алгоритмы, в которых действия осуществляются последовательно друг за другом. Стандартная блок-схема линейного алгоритма приводится на рис. 3, а (вычисление произведения двух чисел — А и В).

Разветвляющимся называется алгоритм, в котором действие выполняется по одной из возможных ветвей решения задачи, в зависимости от выполнения условий. В отличие от линейных алгоритмов, в которых команды выполняются последовательно одна за другой, в разветвляющиеся алгоритмы входит условие, в зависимости от выполнения или невыполнения которого выполняется та или иная последовательность команд (действий).

В качестве условия в разветвляющемся алгоритме может быть использовано любое понятное исполнителю утверждение, которое может соблюдаться (быть истинно) или не соблюдаться (быть ложно). Такое утверждение может быть выражено как словами, так и формулой. Таким образом, алгоритм ветвления состоит из условия и двух последовательностей команд.

Примером может являться разветвляющийся алгоритм, изображен­ный на рис. 3, б. Аргументами этого алгоритма являются числа А и B, а результатом — число X. Если условие А >= B истинно, то выполняет­ся операция умножения чисел (Х=А * B), в противном случае выполня­ется операция сложения (X = А + B). В результате печатается то значение, которое получается в результате выполнения одного из действий.

Циклическим называется алгоритм, в котором некоторая часть операций (тело цикла — последовательность команд) выполняется много­кратно. Однако слово «многократно» не значит «до бесконечности». Организация циклов, никогда не приводящая к остановке в выполнении алгоритма, является нарушением требования его результативности — получения результата за конечное число шагов.

Перед операцией цикла осуществляются операции присвоения начальных значений тем объектам, которые используются в теле цикла. В цикл входят в качестве базовых следующие структуры: блок проверки условия и блок, называемый телом цикла. Если тело цикла расположено после проверки условий (рис. 2, в — цикл с предусловием), то может случиться, что при определенных условиях тело цикла не выполнится ни разу. Такой вариант организации цикла, управляемый предусловием, называется циклом типа пока (здесь условие — на продолжение цикла). Возможен другой случай, когда тело цикла выполняется, по крайней мере, один раз и будет повторяться до тех пор, пока не ста­нет истинным условие. Такая организация цикла, когда его тело рас­положено перед проверкой условия, носит название цикла с пост­условием, или цикла типа до (рис. 2, г). Истинность условия в этом случае — условие окончания цикла. Отметим, что возможна ситуация с постусловием и при организации цикла-пока. Итак, цикл-до завершается, когда условие становится истинным, а цикл-пока — когда условие становится ложным. Современные языки программирования имеют достаточный набор операторов, реализующих как цикл-пока, так и цикл-до.

Рассмотрим циклический алгоритм типа пока (рис. 2, в) на при­мере алгоритма вычисления факториала. N — число, факториал которого вычисляется. Начальное значение N! принимается равным 1. К будет меняться от 1 до N и вначале также равно 1. Цикл будет выполняться, пока справедливо условие N ≤ К. Тело цикла состоит из двух операций N!=N! *К и К = К+ 1 (рис. 3, в). Циклические алгоритмы, в которых тело цикла выполняется задан­ное число раз, реализуются с помощью цикла со счетчиком. Цикл со счетчиком реализуется с помощью рекурсивного увеличения значения счетчика в теле цикла (К = К + 1 в алгоритме вычисления факториала).

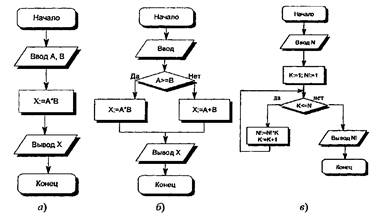
Рис. 3. Примеры структур алгоритмов: а — линейный алгоритм; б — алгоритм с ветвлением; в — алгоритм с циклом

Процесс решения сложной задачи довольно часто сводится к решению нескольких более простых подзадач. Соответственно процесс разработки сложного алгоритма может разбиваться на этапы составления отдельных алгоритмов, которые называются вспомогательными. Каждый такой вспомогательный алгоритм описывает решение какой-либо подзадачи. Процесс построения алгоритма методом последовательной детализации состоит в следующем. Сначала алгоритм формулируется в «крупных» блоках (командах), которые могут быть непонятны исполнителю (не входят в его систему команд) и записываются как вызовы вспомогательных алгоритмов. Затем происходит детализация, и все вспомогательные алгоритмы подробно расписываются с использованием команд, понятных исполнителю.

Дата добавления: 2014-01-07