Примеры и решения. 1.Рассмотрим следующую известную задачу: имеются два кувшина емкостью 3 и 8 л

1. Рассмотрим следующую известную задачу: имеются два кувшина емкостью 3 и 8 л. Необходимо составить алгоритм, с помощью которого, пользуясь только этими двумя кувшинами, можно набрать 7 л воды.

Можно предположить, что кувшин емкостью 3 л необходимо использовать для того, чтобы отлить в него 1 л из полного кувшина емкостью 8 л. Таким образом, решение задачи сводится к поиску возможности поместить, например, 2 л воды в трехлитровый кувшин, затем на­полнить восьмилитровый и перелить из него воду в трехлитровый кувшин, в котором до полного заполнения не хватает, ровно 1 л. Задача реализуется следующим линейным алгоритмом (А — количество воды в трехлитровом кувшине, В — количество воды в восьмилитровом кувшине):

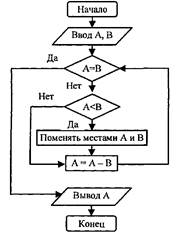
2. Рассмотрим задачу вычисления наибольшего общего делителя (НОД) двух натуральных чисел А и В с применением алгоритма Евкли­да. Основная идея алгоритма в том, что НОД А и В есть также и НОД (А - В), т.е. последовательное вычитание из большего числа меньшего до тех пор, пока числа не сравняются, должно привести к искомому значению НОД.

Приведем сначала запись алгоритма Евклида на естественном языке:

1. Рассмотреть А как первое число, В как второе. Перейти к пункту 2.

2. Сравнить первое и второе число. Если они равны, перейти к пункту 5. Если
нет, перейти к пункту 3.

3. Если первое число меньше второго, то поменять их местами. Перейти к
пункту 4.

4. Вычесть из первого числа второе и рассмотреть полученную разность как
первое число. Перейти к пункту 2.

5. Рассмотреть первое число как результат. Закончить выполнение алгоритма.

Представленный алгоритм имеет разветвляющуюся структуру и в виде блок-схемы изображается следующим образом:

3. Пусть необходимо вывести на печать все числа ряда Фибоначчи (1, 1, 2, 3, 5, 8,...) до заданного натурального N.

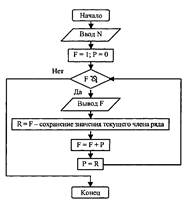
Очередной член ряда F_i определяется как сумма двух предыдущих (F_i = F_i-1 + F_i-2). Первые два члена ряда равны 1.

Представим блок-схему алгоритма решения задачи с использованием циклической структуры с предусловием (F — очередной член ряда, Р — предыдущий член ряда).

Алгоритм решения этой задачи с использованием циклической структуры с постусловием предлагается разработать самостоятельно.

Вопросы и задания

1. Охарактеризуйте базовые структуры алгоритмов.

2. Дано число X и последовательность действий:

• умножить полученное число на 2;

• сообщить результат;

• разделить X на 3;

• вычесть из полученного числа 5;

• прибавить к полученному числу 7.

Сколько и каких различных алгоритмов можно составить из этой последовательности действий? Какие функции от X при этом вычисляются?

3. Приведите примеры задач, для реализации которых применимы: а) линейные алгоритмы; б) разветвляющиеся алгоритмы; в) циклические алгоритмы.

4. Охарактеризуйте разницу между циклом типа до и циклом типа пока.

5. Приведите примеры задач, для реализации которых целесообразно применять циклические структуры: а) с постусловием; б) с предусловием.

6. Изобразите блок-схему алгоритма определения максимального числа в последовательности из п произвольных чисел.

7. Нарисуйте блок-схему алгоритма получения произведения п произвольных чисел (л = 15).

8. Нарисуйте блок-схему алгоритма вычисления суммы квадратов первых п чисел натурального ряда.

9. Модифицируйте алгоритм вычисления суммы квадратов первых п чисел натурального ряда для вычисления суммы квадратов: а) только четных чи­сел (до n); б) только нечетных чисел (до п).

Дата добавления: 2014-01-07