Графический метод решения задачи линейного программирования

Графический метод применяется для решения стандартной задачи линейного программирования с двумя независимыми переменны ми:

найти наибольшее и наименьшее значения функции

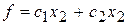(4)

при ограничениях

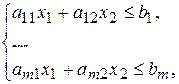(5)

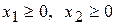. (6)

Геометрическая постановка ЗЛП с двумя переменными: найти в области допустимых решений угловую точку, через которую проходит линия уровня 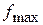(или 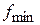), соответствующая наибольшему (наименьшему) значению целевой функции .

При использовании графического метода применяются линии уровня и градиент.

Для линейной функции 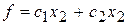вектор градиент 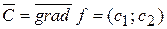, координатами которого являются коэффициенты в целевой функции, показывает направление наискорейшего изменения целевой функции.

Линией уровня функции называется множество всех точек 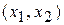, в которых функция принимает постоянное значение. Для функции 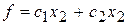линии уровня 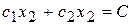- это прямые, перпендикулярные градиенту.

Алгоритм графического метода решения задачи линейного программирования (ЗЛП).

1. Построить область допустимых решений (ОДР) задачи в соответствии с системой неравенств .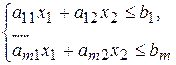

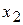
В

A

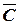
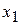
Рисунок 1 – Графический метод решения задачи

2. Строим градиент 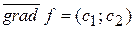и перпендикулярно ему линию уровня – прямую .

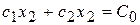3. Линию целевой функции (линия уровня) перемещаем по направлению градиента для задачи на максимум целевой функции и в противоположном направлении - для задач на минимум целевой функции.

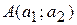4. Параллельным перемещением линии уровня в направлении вектора найдем первую точку «встречи» прямой с ОДР. Это – точка минимума целевой функции . Значение функции является наименьшим значением функции в ОДР.

5. Продолжая передвигать линию уровня, найдем последнюю точку 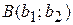выхода прямой из ОДР. Это - точка максимума целевой функции .

6. Если окажется, что линия уровня совпадает с одной из сторон ОДР, то задача ЛП будет иметь бесчисленное множество решений. Если ОДР представляет неограниченную область, то целевая функция – неограниченна. Задача ЛП может быть неразрешима, когда определяющие ее ограничения окажутся противоречивыми.

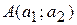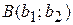7. Находим координаты точки экстремумадля или для 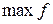и вычисляем значение целевой функции в этой точке.

Пример 2. Найти наибольшее и наименьшее значения функции 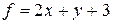в области решений системы линейных неравенств

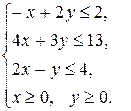
1. Построим область решений системы линейных неравенств.

у

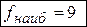
1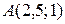

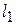
О 2 x

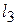
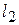
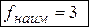
Рисунок 2 – Графическое решение ЗЛП

Прямая (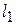) 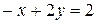, точки для построения и . Так как 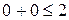верно, то полуплоскость обращена в сторону точки .

Прямую (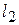) строим по точкам и ; неравенство 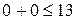верное, полуплоскость направлена к началу координат.

Прямая (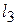) 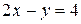построена по точкам 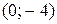и ; полуплоскость обращена в сторону .

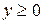Неравенства и показывают, что искомая область (пересечение всех полуплоскостей) находится в первой координатной четверти.

2. Построим градиент функции 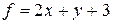. Это вектор с координатами 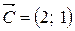с началом в точке 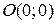. Перпендикулярно градиенту построим линию уровня функции.

3. Параллельным движением линии уровня в направлении градиента 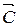найдем точку «входа» линии уровня в область – это точка О(0,0). Вычислим значение функции в этой точке: .

4. Продолжая движение линии уровня в направлении градиента 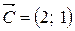, найдем точку «выхода» линии уровня из области – это точка А. Для определения ее координат решим систему уравнений прямых 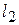и 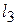, пересекающихся в точке А: 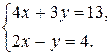Решение системы уравнени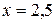й и .

5. Вычислим значение функции в точке : .

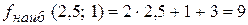Ответ: , .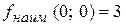

Дата добавления: 2014-01-07