Принятие управленческого решения в экономической задаче

Пример 3. В районе лесного массива имеется лесопильный завод и фабрика, на которой изготавливают фанеру. Чтобы деревообрабатывающему комбинату получить 1 м³ пиломатериалов, необходимо израсходовать 4 м³ еловых и 2 м³ пихтовых материалов. Для изготовления 1 м² фанеры требуется 3 м³ еловых и 5 м³ пихтовых материалов. Лесной массив содержит 1200 м³ еловых и 1000 м³ пихтовых материалов.

В течение планируемого периода нужно произвести не менее 50 м³ пиломатериалов и 100 м² фанеры. Доход с одного м³ пиломатериалов составляет 15 ден. ед., а с 1 м² фанеры – 10 ден. ед.

Какое количество пиломатериалов и фанеры должен произвести деревообрабатывающий комбинат, чтобы получить наибольшую прибыль?

Решение

Составим математическую модель задачи.

Пусть 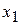(м³) – количество пиломатериалов, 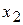(м²) – количество фанеры, которые должен произвести комбинат. Очевидно, на эти переменные необходимо наложить условие неотрицательности: , . Кроме того, запасы лесоматериалов ограничены, откуда получаем условия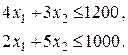

К ним добавляются ограничения на плановые задания: х ₁ ³ 100 и х ₂ ³ 50.

По условию задачи требуется произвести пиломатериалов и фанеры столько, чтобы это принесло наибольшую прибыль: .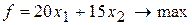

Таким образом, получаем задачу линейного программирования:

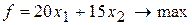
С геометрической точки зрения, необходимо найти наибольшее значение функции 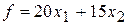в области решений системы неравенств

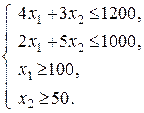
1. Построим область решений системы неравенств

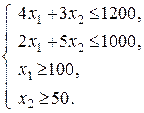
Для этого построим граничные прямые

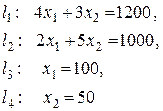
(рисунок 3). Каждая из этих прямых делит координатную плоскость на две полуплоскости.

Чтобы выяснить, какую полуплоскость определяет неравенство 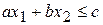, нужно взять произвольную точку М(х ₀, у ₀) плоскости, не лежащую на прямой 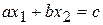, и подставить ее координаты в неравенство 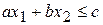. Если при этом получится верное числовое неравенство, то полуплоскость, содержащая взятую точку, и есть искомая область решений неравенства. Если же координаты точки не удовлетворяют неравенству, решением неравенства являются все точки второй полуплоскости.

Легко проверить, что координаты точки М(200;100) удовлетворяют всем неравенствам системы, следовательно, область допустимых решений есть четырехугольник АВСD.

2. Построим градиент целевой функции f = 20 x ₁ +15 x ₂. Имеем

.

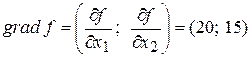На рисунке 4 изображен вектор `N, параллельный градиенту функции f.

3. Линии уровня целевой функции имеют уравнения – это уравнение прямых

4. на плоскости.

Чтобы построить одну из них, придадим С произвольное значение, например, С = 0. Получим прямую 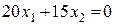, проходящую через начало координат.

Заметим, что линии уровня перпендикулярны градиенту функции.

4. Найдем наибольшее значение функции f = 20 x ₁ +15 x ₂ в построенной области. Для этого, передвигая линию уровня параллельно самой себе в направлении вектора `N, находим точку «выхода» из области допустимых решений АВСD, которой соответствует наибольшее значение целевой функции f в области допустимых решений.

В нашем случае точкой «входа» является точка А (но нас она не интересует, т.к. мы ищем наибольшее значение функции f). Точками «выхода» из области АВСD являются точки отрезка СD прямой l ₁ (прямые 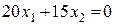и параллельны), поэтому наибольшего значения функция f = 20 x ₁ +15 x ₂ достигает во всех точках этого отрезка, что является признаком альтернативного оптимума.

Итак, каждая точка отрезка СD является оптимальным решением задачи, т е. в каждой точке этого отрезка функция принимает наибольшее в области АВСD значение. Найдем это значение.

Сначала найдем координаты точек С и D.

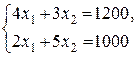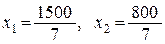С: Þ , С.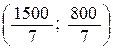

Полученные значения переменных х ₁ и х ₂ соответствуют найденному выше опорному решению 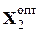. Значение целевой функции в этой точке

.

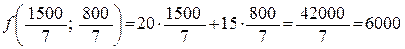Аналогично: D: Þ 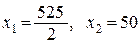, D(262,5; 50).

Эти значения переменных х ₁ и х ₂ соответствуют опорному решению 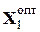, значение целевой функции в точке D равно

.

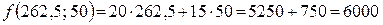Итак, мы на примере проиллюстрировали известный факт: опорные решения ЗЛП соответствуют угловым точкам области допустимых решений задачи. А оптимальное решение совпадает, по крайней мере, с одним из опорных решений.

Чтобы получить наибольшую прибыль 6000 ден.ед., следует произвести из имеющихся материалов 262,5 м³ пиломатериалов и 50 м² фанеры.

Контрольные вопросы

1. В чем состоит содержание процесса постановки задачи?

2. Какие существуют виды задач принятия оптимальных решений?

3. Что такое экономико-математическая модель задачи?

4. Каков порядок действий построения математической модели экономической задачи?

5. Какой экономический смысл могут иметь переменные, участвующие в математических моделях?

6. Какой экономический смысл могут иметь ограничения вида 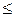; ; в математических моделях распределительной задачи и задачи об использовании сырья? Укажите возможный экономический смысл левых и правых частей этих ограничений.

7. Приведите экономические примеры целевых функций , и укажите содержательное значение переменных и коэффициентов при них.

8. Сформулируйте общую задачу математического программирования и запишите ее математическую модель.

9. Сформулируйте общую задачу линейного программирования и запишите ее математическую модель.

10. Запишите задачу линейного программирования в канонической и стандартной формах.

11. С помощью каких преобразований можно перейти от общей или стандартной формы задачи линейного программирования к канонической?

12. Дайте определение допустимого и оптимального решений задачи линейного программирования.

13. Дайте геометрическую постановку ЗЛП с двумя переменными.

14. Укажите последовательность действий для нахождения наибольшего и наименьшего значений функции в замкнутой области.

15. Как построить полуплоскость, заданную линейным неравенством с двумя переменными ?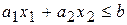

16. Запишите для линейной функции 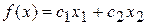вектор градиент, назовите вид линий уровня. Как расположены относительно друг друга градиент и линии уровня?

17. Как с помощью градиента и линий уровня найти точки наименьшего и наибольшего значений линейной функции в области, заданной системой линейных неравенств? Опишите порядок действий.

18. Как найти координаты точек области, в которых функция принимает наибольшее и наименьшее значения?

19. Сформулируйте алгоритм графического метода решения стандартной ЗЛП с двумя переменными.

Дата добавления: 2014-01-07