Метод потенциалов нахождения оптимального решения

1) Каждому поставщику ставится в соответствие число 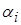, потребителю - число , называемые потенциалами. Значения потенциалов подбираются так, чтобы для всех заполненных клеток выполнялись условия

. (6)

Выбрать переменную 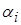или , которой соответствует наибольшее количество занятых клеток, приравнять её к нулю, решить систему уравнений относительно 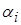и и найти эти значения.

2) Для всех свободных клеток составить и проверить выполнение условия оптимальности плана перевозок

(7)

Если для всех свободных клеток выполняется это неравенство, то тогда найден оптимальный план.

Если хотя бы для одной клетки не выполняется это неравенство, то необходимо улучшить опорный план с помощью коэффициента перераспределения .

3) Находим клетку, где больше всего не выполняется неравенство. Если таких клеток несколько, то выбирается любая. В эту клетку ставим со знаком «+».

4) Построить «цикл» (контур перераспределения груза), начиная с выбранной клетки, исходя из следующих правил:

- В строке и столбце должно быть четное количество ;

- Контур меняет направление только в базисных клетках (заполненных);

- Коэффициент меняет свой знак с «+» на «-» поочередно в углах контура.

5) После построения контура (цикла) отметить, в каких заполненных клетках коэффициент стоит с отрицательным знаком. Из этих клеток найти клетку с наименьшим значением перевозки, коэффициент будет равен перевозке в выбранной клетке. Найти новый план, перераспределив найденное значение по контуру с учетом знаков «+» и «-», прибавляя или уменьшая стоящую в клетке перевозку. Это число прибавляем к поставкам в клетках со знаком "+" и вычитаем это же число из поставок в клетках со знаком "–".

6) Проверить новый планна оптимальность в соответствии в п.2. Если неравенства не выполняются, то повторяются действия, начиная с пункта 3.

7) Если неравенства для свободных клеток выполняются, значит найденный план оптимален. Вычисляется стоимость оптимального плана перевозок.

Замечания.

· Для любой свободной клетки можно построить только один цикл.

· Потенциалы, как и циклы, для каждого решения определяются заново.

· Если при перемещении по циклу числа освободится сразу несколько клеток, то одну из освобождающихся клеток (которой соответствует наибольшая стоимость перевозок 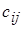) оставляют свободной, а другие заполняют нулями (получается так называемое вырожденное решение).

· При переходе от решения 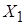к решению значение целевой функции изменится на величину (8), где - число, перемещаемое по циклу, составленному для клетки с отрицательной оценкой .

Задача 2. Решить транспортную задачу.

Таблица 4

Запасы груза	Потребности в грузе

Дата добавления: 2014-01-07