Решение. 1) Проверим условие разрешимости транспортной задачи:

1) Проверим условие разрешимости транспортной задачи:

; .

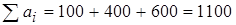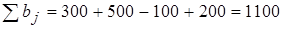Таким образом, ТЗ закрытая и, следовательно, имеет оптимальное решение.

2) Запишем математическую модель ТЗ.

Обозначим через 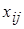количество перевезенного груза из 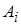(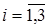) в 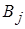(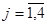), при этом 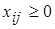. Составим систему ограничений:

условия вывоза груза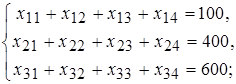

условия доставки груза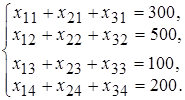

Суммарные затраты на перевозку груза равны

.

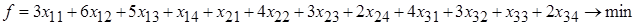Требуется найти такое неотрицательное решение 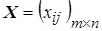системы ограничений, при котором функция 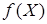принимает наименьшее значение.

3) Построим исходное опорное решение 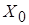методом «минимального элемента».

Последовательность заполнения клеток в распределительной таблице следующая: (2,1), (1,4), (3,3), (3,4), (3,2), (2,2).

Таблица 5

Запасы груза	Потребности в грузе

В плане перевозок число заполненных клеток равно m + n – 1 = 3 + 4 – 1 = 6. Транспортные расходы составляют _.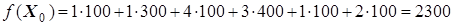

4) Найдем потенциалы 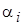и .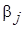

Найдем потенциалы 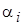и 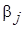из системы уравнений, составленных для заполненных клеток.

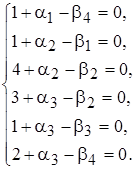
В системе число уравнений 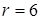меньше числа неизвестных 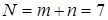, поэтому система имеет бесконечное множество решений, при этом число свободных неизвестных равно 7 – 6 = 1.

Придадим неизвестной 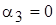(она чаще всего встречается в системе) произвольное значение. Тогда остальные потенциалы равны:

; ; ; ; ; ; .

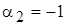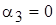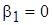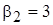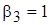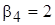5)Проверим решение 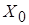на оптимальность.

Вычислим оценки свободных переменных, соответствующих свободным клеткам:

D11 = с 11 + a1 – b1 = 3 + 1 – 0 = 4;	D12 = с 12 + a1 – b2 = 6 + 1 – 3 = 4;
D13 = с 13 + a1 – b3 = 5 + 1 – 1 = 5;	D23 = с 23 + a2 – b3 = 3 –1 – 1 = 1;
D24 = с 24 + a2 – b4 = 2 – 1 – 2 = – 1;	D31 = с 31 + a3 – b1 = 4 + 0 – 0 = 4.

Оценка 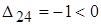, поэтому план перевозок 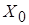не оптимален и транспортные расходы не являются наименьшими.

Дата добавления: 2014-01-07