
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Графический способ нахождения оптимальных стратегий ЛПР
|
|
|
|
Если седловой точки нет, то можно применить графический способ или составить модель и решить симплекс-методом.
Геометрический способ решения игр с нулевой суммой применяется к играм, где хотя бы у одного игрока только две стратегии. Если же игра не сводится путем упрощения к размерности 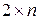 или
или 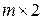 , то составляется математическая модель и задача решается симплекс-методом.
, то составляется математическая модель и задача решается симплекс-методом.
Пример 3. Рассмотрим платежную матрицу, у которой нет седловой точки (проверить!). Значит, игроки будут применять смешанные стратегии.
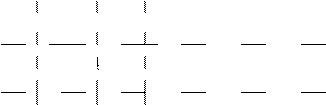 |
Упростим матрицу, вычеркивая заведомо невыгодные стратегии игроков. Путем упрощения, ее можно свести к матрице 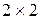 .
.
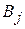 
| 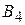 ( (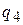 ) )
| 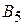 ( (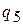 ) )
|
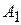 ( (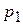 ) )
| ||
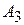 ( ( ) )
|
Рассмотрим решение с позиции игрока А.
Найдем его оптимальную стратегию 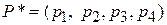 , в которой уже известно, что
, в которой уже известно, что 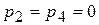 (отброшены доминируемые стратегии А2 и А4).
(отброшены доминируемые стратегии А2 и А4).
Обозначим 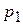 - вероятность применения игроком
- вероятность применения игроком 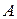 стратегии
стратегии 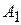 ;
;
 - вероятность применения игроком
- вероятность применения игроком 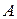 стратегии
стратегии 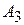 .
.
Так как 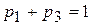 , то
, то 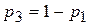 .
.
Тогда получим, что средний выигрыш игрока 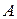 равен цене игры
равен цене игры 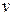 :
:
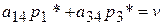 , или
, или 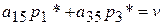 .
.
Чистые стратегии игрока 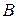
| Ожидаемые выигрыши игрока 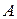
|
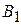
| 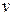 = 4 р1 + 3 р3 = 4р1 + 3(1 - p1) = р1 + 3 = 4 р1 + 3 р3 = 4р1 + 3(1 - p1) = р1 + 3
|
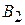
| 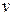 = 2 р1 + 5 р3 = 2 р1 + 5(1-p1) = -3р1 + 5 = 2 р1 + 5 р3 = 2 р1 + 5(1-p1) = -3р1 + 5
|
На оси Ох разместим точки р1=0 и р1=1, через которые проведем прямые, перпендикулярные оси Ох. Подставляя р1=0 и р1=1 в выражение р1+3, найдем значения 3 и 4, которые отложим на соответствующих перпендикулярных прямых. Соединив эти точки, получим прямую.
Аналогично рассмотрим выражение (-3р1+5). Подставляя р1=0 и р1=1 в это выражение, найдем значения 5 и 2, которые отложим на соответствующих перпендикулярных прямых. Соединив эти точки, получим вторую прямую.
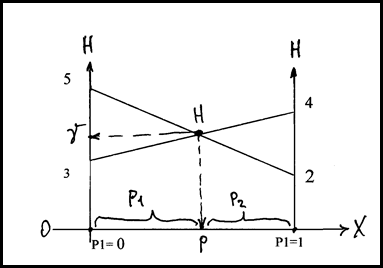
Оптимальная стратегия игрока 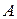 найдется из равенства выражений (р1+3) и (-3р1+5). Отсюда р1=р3=0,5.
найдется из равенства выражений (р1+3) и (-3р1+5). Отсюда р1=р3=0,5.
Оптимальная стратегия  .
.
Цена игры для игрока А равна  .
.
Для второго игрока 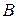 оптимальная стратегия
оптимальная стратегия 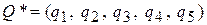 ищется аналогично. Известно, что
ищется аналогично. Известно, что 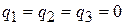 (отброшены доминируемые стратегии В1, В2 , В3).
(отброшены доминируемые стратегии В1, В2 , В3).
Обозначим 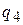 - вероятность применения игроком
- вероятность применения игроком 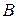 стратегии
стратегии 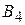 ;
;
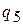 - вероятность применения игроком
- вероятность применения игроком 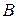 стратегии
стратегии 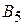 .
.
Так как  , то
, то 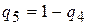 . Зная, что средний выигрыш игрока
. Зная, что средний выигрыш игрока 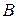 равен цене игры
равен цене игры 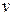 , заполним таблицу.
, заполним таблицу.
Чистые стратегии игрока 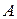
| Ожидаемые выигрыши игрока 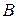
|
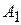
| 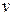 = 4q4 + 2q5 = 4q4 + 2(1 – q4) = 2q4 + 2 = 4q4 + 2q5 = 4q4 + 2(1 – q4) = 2q4 + 2
|
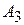
| 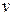 = 3q4 + 5q5 = 3 q4 + 5(1-q4) = -2q4 + 5 = 3q4 + 5q5 = 3 q4 + 5(1-q4) = -2q4 + 5
|
Оптимальная стратегия игрока 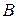 найдется из равенства выражений (2q4+2) и (-2q4+5). Отсюда q4=0,74; q5=0,25, оптимальная стратегия
найдется из равенства выражений (2q4+2) и (-2q4+5). Отсюда q4=0,74; q5=0,25, оптимальная стратегия 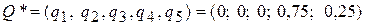 .
.
Цена игры для игрока В равна 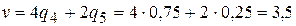 .
.
Ответ:
оптимальное решение игры 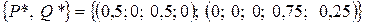 .
.
цена игры 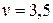 .
.
Контрольные вопросы
1. Чем отличаются проблемы теории игр от проблем теории оптимизации?
2. Что понимается под термином «игра»?
3. В чем состоит основная задача теории игр?
4. Какие парные игры называются матричными? Приведите пример построения платежной матрицы.
5. Что понимается под стратегией игрока?
6. Что значит «решить игру»?
7. Какие встречаются типы игр?
8. Как определяется матричная антагонистическая игра двух лиц?
9. Как находится верхняя и нижняя цена игры для определенной матричной антагонистической игры двух лиц?
10. Всегда ли матричные игры имеют решение в чистых стратегиях?
11. Какая игра называется игрой с нулевой суммой?
12. Что является элементами платежной матрицы игры?
13. Что показывают положительные, нулевые и отрицательные элементы платежной матрицы?
14. В каком случае стратегия игрока 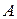 называется оптимальной?
называется оптимальной?
15. В каком случае стратегия игрока 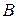 называется оптимальной?
называется оптимальной?
16. Как найти седловой элемент платежной матрицы? Какую роль играет седловой элемент?
17. Какие есть методы решения матричных антагонистических игр?
18. Каковы принципы решения игр в неопределенных ситуациях?
19. Какими способами можно упрощать платежные матрицы?
20. Как определить доминирующие стратегии игрока?
21. Что понимается под играми с природой?
22. Как найти средний выигрыш игрока при известных вероятностях стратегий и при неизвестных вероятностях?
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 678; Нарушение авторских прав?; Мы поможем в написании вашей работы!