
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Примеры решения задач для магнитного поля в вакууме
|
|
|
|
1. По плоскому контуру течет ток силы I=0,5 A. Радиусы колец контура 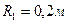 ,
, 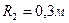 . Найти магнитную индукцию В в точке С (рис.178).
. Найти магнитную индукцию В в точке С (рис.178).
|
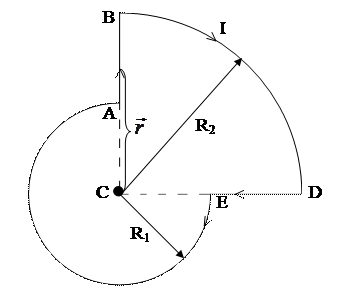
| Рис.178 |
Решение.
Из рис.178 видно, что контур с током можно разбить на следующие участки: АВ; BD; DE; EA.
Векторы индукции от всех участков тока направлены перпендикулярно плоскости чертежа от нас.
Контур с током ЕА является ¾ кругового тока с радиусом  , а контур BD – ¼ кругового тока с радиусом
, а контур BD – ¼ кругового тока с радиусом 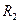 . Поэтому для них используем формулу индукции для кругового тока.
. Поэтому для них используем формулу индукции для кругового тока.
Для ЕА:
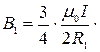 (430)
(430)
Для BD:
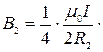
| (431) |
Для прямолинейных участков тока АВ и DE используем формулу расчета индукции В прямолинейного тока конечной длины.
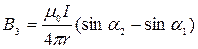 . .
| (432) |
В формуле (432) углы 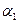 и
и 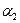 являются углами между направлениями радиуса вектора
являются углами между направлениями радиуса вектора  и током I. Из рис.(178) видно, что
и током I. Из рис.(178) видно, что 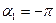 ,
, 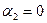 и
и 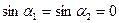 . Поэтому
. Поэтому  . Так же можно рассуждать и для тока DE (
. Так же можно рассуждать и для тока DE (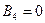 ).
).
Общая индукция в точке С равна
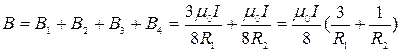 . .
| (434) |
2. Эбонитовый шар радиуса R=0,05 м заряжен равномерно поверхностным зарядом с плотностью 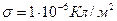 . Шар приводится во вращение вокруг своей оси с угловой скоростью
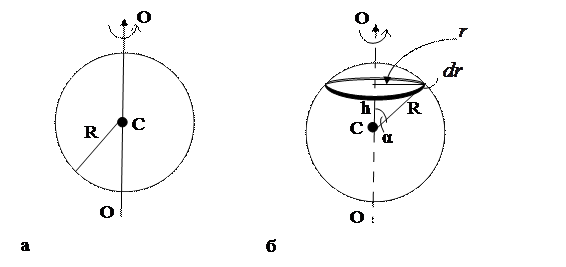
. Шар приводится во вращение вокруг своей оси с угловой скоростью 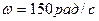 . Найти магнитную индукцию В в центре шара (рис.179а).
. Найти магнитную индукцию В в центре шара (рис.179а).
Решение.
Разбиваем шар на большое число элементарных колец (рис.179б).
Заряд элементарного кольца равен
 . .
| (435) |
При вращении заряд dq вокруг оси ОО создает ток силой
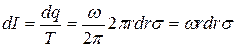 , ,
| (436) |
|
| Рис.179 |
где 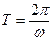 - период обращения шара.
- период обращения шара.
Круговой ток dI в точке С создает магнитное поле, индукция которого определяется формулой
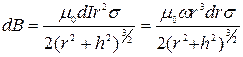 . .
| (437) |
Из рис.179б видно, что 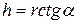 .
.
Тогда
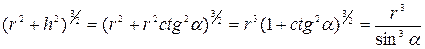 . .
| (438) |
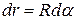 . .
| (439) |
С учетом (438) и (439) выражение (437) запишется в виде
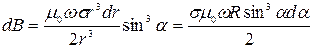 . .
| (440) |
Интегрируя (440), получим индукцию поля в точке С
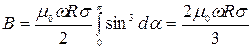 . .
| (441) |
3. Медный провод сечением 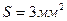 , согнутый в виде трех сторон квадрата, может вращаться относительно горизонтальной оси. Провод находится в однородном магнитном поле. Когда по проводу течет ток силой I=15 A, провод отклоняется на угол
, согнутый в виде трех сторон квадрата, может вращаться относительно горизонтальной оси. Провод находится в однородном магнитном поле. Когда по проводу течет ток силой I=15 A, провод отклоняется на угол 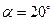 . Определите индукцию магнитного поля (рис.180).
. Определите индукцию магнитного поля (рис.180).
Решение.
На проводник с током (CD) в магнитном поле В действует сила Ампера
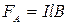
| (442) |
и сила тяжести
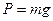 , ,
| (443) |
моменты сил которых уравновешивает проводник.
Сила Ампера, действующие на токи, текущие по сторонам АС и DB, равны по ве
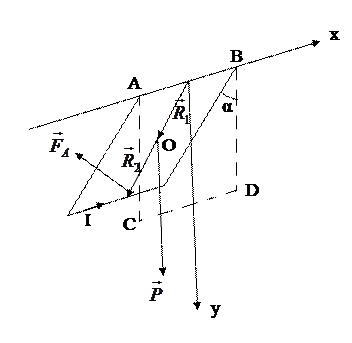
|
| Рис.180 |
личине и противоположны по направлению, радиус-векторы этих сил одинаковы, и поэтому суммарный момент сил, действующих на эти части проводника, равен нулю. Поэтому в (442) l – длина проводника CD. Масса всего проводника равна
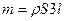 , (444)
, (444)
где 3l – длина всего проводника, т.к. AC=BD=CD=l.
С учетом (3) сила тяжести равна
 (445)
(445)
и она приложена в точке О, которая является центром масс. Координаты центра масс относительно оси Х определяются формулой
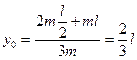 и
и 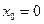 . (446)
. (446)
Тогда длина радиуса вектора 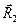 точки О относительно оси Х равен
точки О относительно оси Х равен
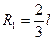 . (447)
. (447)
Момент силы тяжести Р относительно оси Х равен
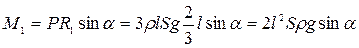 . .
| (448) |
Момент силы Ампера, действующий на проводник с током CD, равен
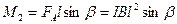 , ,
| (449) |
где 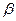 - угол между векторами
- угол между векторами 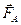 и
и 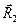 ,
, 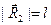 .
.
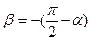 . .
| (450) |
С учетом (450) формула (449) запишется в виде
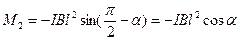 . .
| (451) |
Момент силы 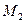 направлен противоположно моменту силы
направлен противоположно моменту силы 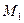 . Приравняв (451) и (448), получим
. Приравняв (451) и (448), получим
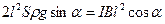 или или 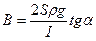 . .
| (452) |
4. Две бесконечно длинные прямолинейные параллельные токи расположены на расстоянии d=5 см друг от друга. Найти индукцию магнитного тока в точке С, удаленной от первого тока на расстояние 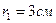 , от второго – на
, от второго – на 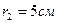 , если силы тока равны
, если силы тока равны 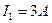 и
и 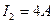 (рис.181).
(рис.181).
Решение.
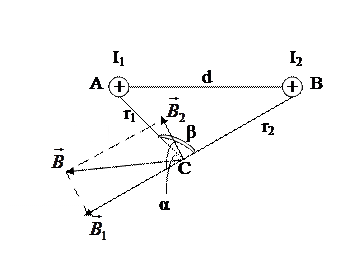
Пусть токи направлены перпендикулярно плоскости чертежа от нас (рис.181). Векторы индукции, поля создаваемого каждым током, направлены как показано на
|
| Рис.181 |
рис.181. Тогда результирующая индукция равна
 . (453)
. (453)
Для прямолинейного тока индукцию находим по формуле
 и
и 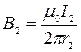 . (454)
. (454)
Угол 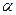 находим, используя теорему косинусов
находим, используя теорему косинусов
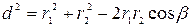
и
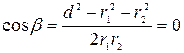 ;
; 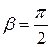 .
.
Тогда
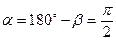 . .
| (455) |
С учетом (454) и (455) находим B по формуле (453)
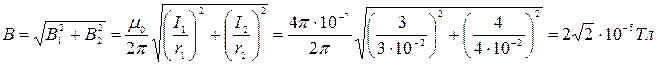 .
.
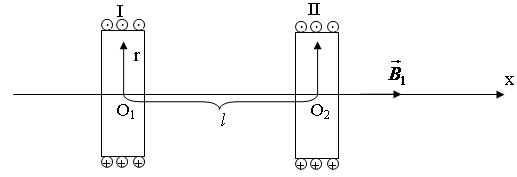
5. Две небольшие одинаковые катушки расположены так, что их оси лежат на одной прямой (рис.182). Расстояние между катушками 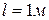 значительно превыша-
значительно превыша-
|
| Рис.182 |
ет их линейные размеры. Число витков каждой катушки N= 100, радиус витков 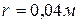 . С какой силой F взаимодействуют катушки, когда по ним течет одинаковый ток I= 1 A?
. С какой силой F взаимодействуют катушки, когда по ним течет одинаковый ток I= 1 A?
Решение.
Магнитное поле, создаваемое I катушкой в точке О2 определяется формулой для индукции кругового тока на оси в любой точке умноженное на число витков (рис.182)
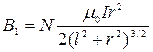 . .
|
Катушка 2 обладает магнитным моментом, который равен
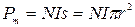 , ,
| (456) |
где 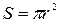 - площадь сечения катушки.
- площадь сечения катушки.
Тогда на магнитный момент со стороны поля действует сила, равная
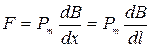 . .
| (457) |
Подставляя (455) и (456) в (457) и с учетом, что 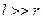 , получим
, получим
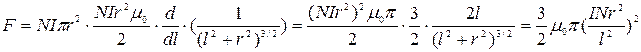 . .
| (458) |
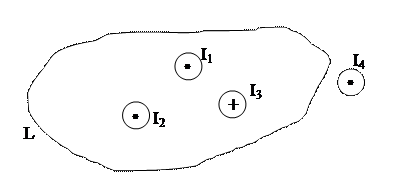
6. Чему равна циркуляция вектора магнитной индукции В произвольного контура, охватываемого током (рис.183)?
|
| Рис.183 |
Решение.
По теореме циркуляции вычисляется формулой
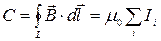 . (459)
. (459)
Условно токи, текущие от нас к плоскости чертежа с плюсом, на нас – со знаком минус. Токи, находящиеся вне контура, циркуляция равна нулю. Поэтому 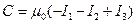 .
.
7. Однородное поле с индукцией 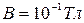 помещена квадратная рамка со сто- роной a=0,05 м, имеющая N=10 витков. Плоскость рамки составляет с направлением магнитного поля угол
помещена квадратная рамка со сто- роной a=0,05 м, имеющая N=10 витков. Плоскость рамки составляет с направлением магнитного поля угол 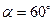 .
.
Определите:
1) магнитный поток, пронизывающий рамку;
2) работу, совершаемую магнитным полем при повороте рамки к положению

|
| Рис. 184 |
равновесия, если по виткам про пустить ток I= 10 А (рис.184).
Решение.
1. Магнитный поток рамки определяется формулой
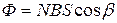 , (460)
, (460)
где S – площадь рамки
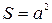 ; (461)
; (461)
N – число витков рамки;
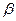 - угол между векторами
- угол между векторами 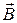 и
и 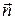 - нормалью рамки.
- нормалью рамки.
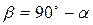 . .
| (462) |
С учетом (461) и (462) получим
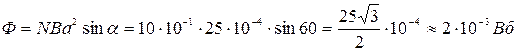 . .
|
Магнитный момент рамки равен
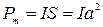 . .
| (463) |
На магнитный момент 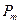 со стороны поля действует момент силы
со стороны поля действует момент силы
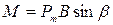 , ,
| (464) |
которая совершает работу
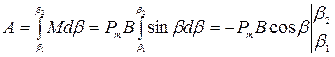 . .
| (465) |
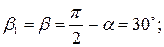
 .
.
Тогда работа равна
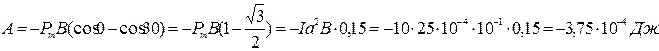
8. Виток, по которому течет ток 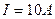 , свободно установился в однородном магнитном поле с индукцией В=0,02 Тл. Диаметр витка
, свободно установился в однородном магнитном поле с индукцией В=0,02 Тл. Диаметр витка 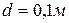 . Какую работу нужно совершить: а) по перемещению витка в область пространства без магнитного поля; б) для поворота витка на угол
. Какую работу нужно совершить: а) по перемещению витка в область пространства без магнитного поля; б) для поворота витка на угол  относительно оси, совпадающей с диаметром?
относительно оси, совпадающей с диаметром?
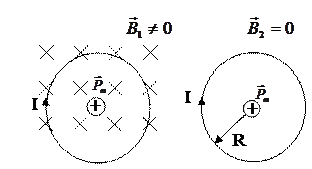
|
| Рис.185 |
Решение.
а) Работа, совершаемая силой тока, определяется формулой
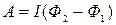 , (466)
, (466)
Ф1 и Ф2 – магнитные потоки, пронизывающие виток в начальном и конечном положениях (рис.185). Магнитный поток определяется формулой
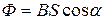 , (467)
, (467)
где 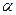 - угол между векторами нормали витка и индукцией
- угол между векторами нормали витка и индукцией 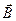 . В данной задаче
. В данной задаче 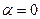 , т.к. вектор нормаль
, т.к. вектор нормаль 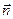 совпадает с вектором индукции
совпадает с вектором индукции 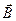 . Поэтому с учетом (467) работа (466) вычисляется формулой
. Поэтому с учетом (467) работа (466) вычисляется формулой
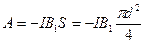 , ,
| (468) |
где 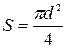 - площадь витка.
- площадь витка.
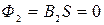 , т.к.
, т.к.  . Подставляя численные значения, получим
. Подставляя численные значения, получим
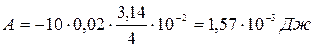 .
.

|
| Рис.186 |
Знак (-) показывает, что работа совершается внешними силами.
б) При повороте витка момент силы, действующий на виток, совершает работу (рис.186)
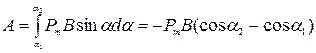 , (469)
, (469)
где 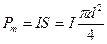 - магнитный момент витка. Из рис.186 видно, что
- магнитный момент витка. Из рис.186 видно, что  . По условию задачи
. По условию задачи 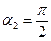 . Поэтому работа равна
. Поэтому работа равна
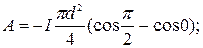
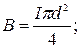

9. Тороид прямоугольного сечения содержит N=500 витков. Наружный диаметр тороида D=0,4 м, внутренний d=0,2 м. Ток, текущий по обмотке, I=2 A. Опреде
|
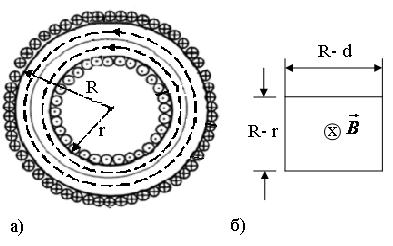
| Рис187 |
лите: а) максимальное и минимальное значение индукции в тороиде; б) магнитный поток через сечение тороида.
Решение.
На рис.187а пунктирной линией показана силовая линия магнитного поля, а на
рис.187б – сечение тороида. Индукция поля внутри тороида определяется формулой
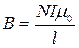 , (470)
, (470)
где l – длина тороида.
Если 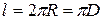 , то индукция минимальна и равна
, то индукция минимальна и равна
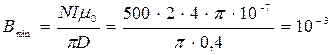 Тл.
Тл.
Если 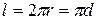 , то индукция максимальна и равна
, то индукция максимальна и равна
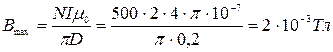 . .
| (471) |
Магнитный поток через сечение тороида определяется
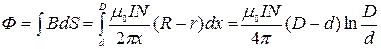 , ,
| (472) |
где 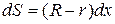 - элементарная площадь, через которую пронизывает магнитный поток.
- элементарная площадь, через которую пронизывает магнитный поток.
10. Протон и электрон, имеющие одинаковую скорость, попадают в однородное магнитное поле, индукция которого 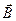 перпендикулярна скорости зарядов. Как будут отличаться траектории заряженных частиц?
перпендикулярна скорости зарядов. Как будут отличаться траектории заряженных частиц?
Решение.
На заряженные частицы будет действовать сила Лоренца (рис.188)

|
| Рис.188 |
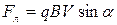 , (473)
, (473)
где q, V – заряд и скорость частицы. По условию задачи 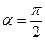 - угол между векторами
- угол между векторами 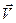 и
и 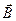 . Поэтому (473) запишется в виде
. Поэтому (473) запишется в виде
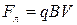 . (474)
. (474)
Под действием силы 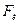 частицы будут двигаться по траектории окружности (на рис.188 верхняя траектория для протона, нижняя – для электрона).
частицы будут двигаться по траектории окружности (на рис.188 верхняя траектория для протона, нижняя – для электрона).
По второму закону Ньютона
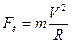 или или 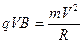 или или 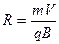 . .
| (475) |
Из (475) видно, что при одинаковых V, q, B радиус кривизны зависит от массы m частицы. Т.к. масса 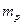 протона примерно 1800 раз больше массы электрона, то радиус кривизны протона на 1800 раз больше, чем радиус кривизны электрона.
протона примерно 1800 раз больше массы электрона, то радиус кривизны протона на 1800 раз больше, чем радиус кривизны электрона.
11. Протон, имеющий скорость 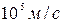 , влетает в однородное магнитное поле с индукцией
, влетает в однородное магнитное поле с индукцией 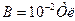 под углом
под углом 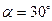 к ее направлению. Определите радиус, пе
к ее направлению. Определите радиус, пе
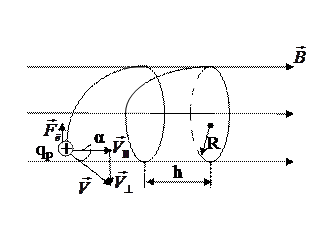
|
| Рис.189 |
риод обращения и шаг винтовой линии, по которой будет двигаться протон. Масса протона 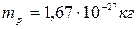 , заряд
, заряд 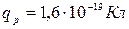 .
.
Решение.
Скорость 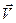 протона можно разложить на
протона можно разложить на 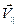 - составляющая скорость параллельна линиям индукции и
- составляющая скорость параллельна линиям индукции и 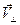 - составляющая скорость перпендикулярна линиям индукции (в данном случае она направлена на нас от плоскости чертежа рис.189).
- составляющая скорость перпендикулярна линиям индукции (в данном случае она направлена на нас от плоскости чертежа рис.189).
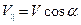 и и 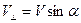 . .
| (476) |
На протон действует сила Лоренца, которая равна 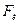 (см. на рис.187)
(см. на рис.187)
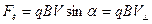 . .
| (477) |
По второму закону Ньютона
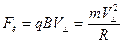 ,
,
и радиус траектории равен
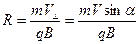 . .
| (478) |
Период обращения равен
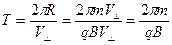 . .
| (479) |
Он не зависит от скорости частицы.
Так как частица обладает продольной скоростью  , то она будет двигаться по винтовой траектории. Поэтому за время Т протон перемещается вдоль поля расстояние, равное
, то она будет двигаться по винтовой траектории. Поэтому за время Т протон перемещается вдоль поля расстояние, равное
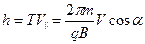 . .
| (480) |
Подставляя численные значения, получим
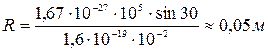
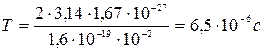
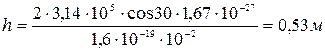 .
.
12. Однородные электрическое (Е= 500 В/м) и магнитное (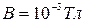 ) поля взаимно перпендикулярны. Какой должна быть скорость электрона по величине и направлению, чтобы его движение было прямолинейным и равномерным? Определите энергию электрона.
) поля взаимно перпендикулярны. Какой должна быть скорость электрона по величине и направлению, чтобы его движение было прямолинейным и равномерным? Определите энергию электрона.
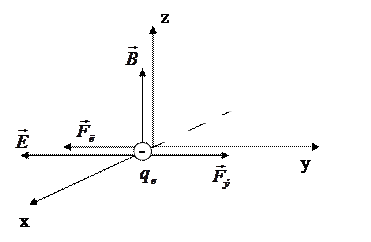
|
| Рис.190 |
Решение.
На электрон действуют электрическая сила (рис.190)
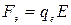 (481)
(481)
и магнитная сила Лоренца
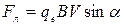 , (482)
, (482)
т.к. 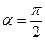 , то
, то
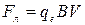 . (483)
. (483)
Для того, чтобы электрон двигался прямолинейно и равномерно сумма всех сил, действующих на него, должна равна нулю, т.е.
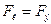
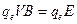 или
или 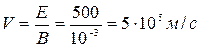 .
.
Энергия электрона равна
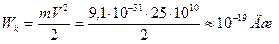 или
или 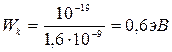 .
.
13. По металлической ленте толщиной 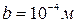 и шириной
и шириной 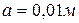 течет ток силой
течет ток силой 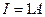 . Лента помещена в магнитное поле с индукцией В=1 Тл перпендикулярно ленте. Определите разность потенциалов между точками А и С (рис.191).
. Лента помещена в магнитное поле с индукцией В=1 Тл перпендикулярно ленте. Определите разность потенциалов между точками А и С (рис.191).

|
| Рис.191 |
Число электронов в единице объема равно 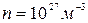 . Заряд электрона
. Заряд электрона 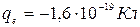 ,
,
масса 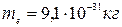 (рис.191).
(рис.191).
Решение.
Холловская разность потенциалов определяется формулой
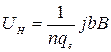 , (484)
, (484)
где 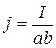 - плотность тока,
- плотность тока, 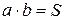 - сечение ленты, а – ширина ленты. Тогда
- сечение ленты, а – ширина ленты. Тогда
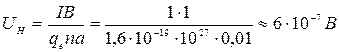 .
.
14. Протон ускоряется электрическим полем напряженностью 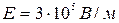 , действующим на протяжении
, действующим на протяжении 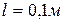 , затем он попадает в однородное магнитное
, затем он попадает в однородное магнитное

| ||||
| Рис.192 |
поле с индукцией В= 1 Тл, действующее в плоскости, перпендикулярной электрическому полю. Определите: а) циклическую частоту вращения протона в магнитном поле, б) радиус траектории вращения протона (рис.192).
Решение.
Работа сил электрического поля по перемещению протона на пути l равна
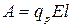 . .
| (485) |
С другой стороны она равна изменению кинетической энергии
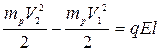 . .
| (486) |
Т.к. начальная скорость 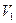 протона равна нулю, то
протона равна нулю, то
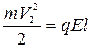 или или 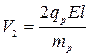 . .
| (487) |
Со скоростью 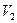 протон влетает в магнитное поле, где на него действует сила Лоренца
протон влетает в магнитное поле, где на него действует сила Лоренца 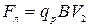 , и движение будет по круговой орбите (рис.192)
, и движение будет по круговой орбите (рис.192)
По второму закону Ньютона 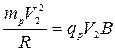 с учетом (487)
с учетом (487)
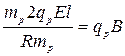 ,
,
находим радиус орбиты 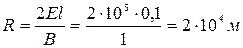 .
.
Период обращения с учетом (487) и радиуса R равен:
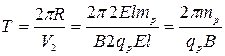 . .
| (489) |
Циклическая частота связана с периодом (489) соотношением
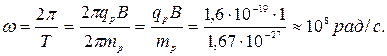
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 3767; Нарушение авторских прав?; Мы поможем в написании вашей работы!