Теория диамагнетизма

Элементарная теория диа- и парамагнетизма

Атомный магнитный момент диамагнетика равен нулю. Это значит сумма орбитальных (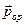) и спиновых (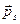) магнитных моментов электронов в атоме равна нулю, т.е.

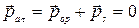(517)

Сначала рассмотрим одноэлектронный атом. По классической теории пусть электрон вращается по орбите вокруг ядра (рис.221). Пусть В=0. На электрон будет действовать кулоновская сила взаимодействия со стороны ядра, которая равна центростремительной силе, т.е.

, (518)

где 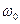- частота вращения электрона, r – радиус орбиты.

Рис.221	Рис.222

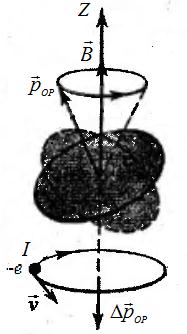
Пусть на атом действует внешнее магнитное поле В (рис.222). Под действием поля на электрон будет действовать дополнительная сила – это сила Лоренца и результирующая сила равна

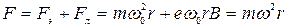или 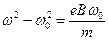. (519)

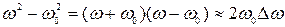, (520)

где ; .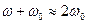

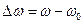С учетом (520) выражение (519) запишется

или 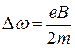. (521)

называется ларморовой частотой.

Под действием магнитного поля орбита электрона будет вращаться с частотой 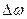вокруг оси Z (прецессия орбиты) (на рис.222 показана пунктирной линией). В результате возникает дополнительный ток и с учетом (521) получим

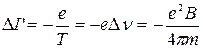, (522)

т.к. .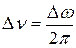

Следовательно возникает дополнительный магнитный момент , который равен

.

(523)

Для многоэлектронного атома имеем

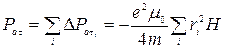. (524)

Т.к. радиус r орбиты электрона меняется с течением времени, т.е. в (524) нужно вместо r² брать среднее значение. Тогда получим

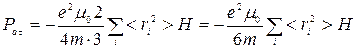. (525)

Тогда намагниченность диамагнетика равна

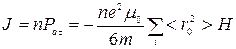, (526)

где n – число атомов в единице объема.

Т.к. , то сравнивая последнее с (526) получим

, (527)

т.е. .

Более точная формула (527) получена Ландау на основе квантовой теории, которая рассматривается за рамками данного курса физики.

Дата добавления: 2014-01-07