Теория парамагнетизма

Впервые в 1905 г. Ланжевен, используя статистику Максвелла-Больцмана, создал классическую теорию парамагнетизма.

Идея следующая. Пусть поле отсутствует В=0. Тогда под действием тепло вой энергии kT магнитные моменты атомов ориентируются беспорядочно (рис.223). Поэтому векторная сумма магнитных моментов равна нулю. Под действием магнитного поля магнитные моменты атомов ориентируются вдоль поля (рис.224) и векторная сумма моментов не равна нулю.

Z Z
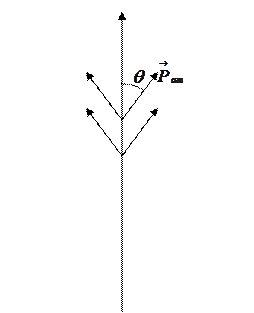
Рис.223	Рис.224

Z

Рис.225

Найдем намагниченность J. Пусть вектор момента ориентируется под углом относительно поля. Из-за тепловой энергии угол будет меняться, т.е. будет происходить дребезжание вектора относительно поля (рис.225).

Тогда вероятность того, что вектор магнитного момента располагается относительно 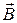в интервале от до , равна

(528)

Проекция момента относительно оси Z равна

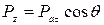(529)

Т.к. 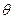меняется (см. выше), то в (529) нужно рассматривать среднее , т.е. 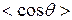. Тогда (529) запишется ввиде

(530)

Ланжевен нашел 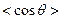в виде

(531)

где . L(x) – называется функцией Ланжевена.

Тогда намагниченность парамагнетика определяется

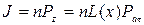, (532)

где n – число атомов в единице объема.

При 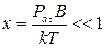функция примет значение

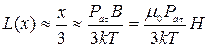. (533)

С учетом (533) намагниченность (532) определяется в виде

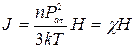, (534)

где 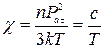(535)

- это магнитная восприимчивость парамагнетика.

Дата добавления: 2014-01-07