КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Операции над множествами
|
|
|
|
После того, как мы научились составлять и различать множества, можно приступить к определению и других операций над ними.
Естественно, что два множества могут иметь одинаковые элементы (их можно выделить в отдельное множество), из всех элементов двух множеств можно составить одно новое множество, также можно рассмотреть отдельно элементы одного множества, которых во втором множестве нет.
Например, А – множество наклеек (марок), которые есть у Пети, В – множество наклеек, которые собрал Вася. Можно выделить множество наклеек, которые есть у обоих ребят; коллекцию различных наклеек, собранных ими вместе; множество наклеек Пети, которых нет у Васи.
Таким образом, мы проделали операции пересечения, объединения и разности двух множеств.
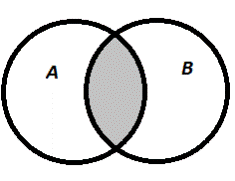
Опр.2.3.1. Пересечением множеств А и В называется множество С, состоящее из всех тех и только тех элементов, которые принадлежат каждому из данных множеств: С={х |хÎА и хÎВ}. Обозначается, А∩В.
Примеры. 1) Пусть A = {1; 2; 3}, B = {2; 3; 4; 5}, D = {10; 11}, тогда A ∩ B = {2; 3}, A ∩ D = Æ.
2) А = {2 n: n Î N } — множество чисел, делящихся на 2, B = {3 n: n Î N} — множество чисел, делящихся на 3, тогда A ∩ B = {6 n | n Î N} — множество чисел, делящихся на 6.
3) А — отрезок [0; 5], В — отрезок [2; 7], тогда A ∩ B — отрезок [2; 5].
4) Студент, сдавший все экзамены на «отлично» получает повышенную стипендию. Сессия состоит из четырех экзаменов. Пусть Аi – множество студентов, сдавших i -й экзамен на «отлично» (i = 1, 2, 3,4), тогда:
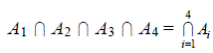
I – множество студентов, получающих повышенную стипендию.
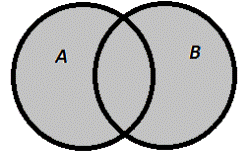
Опр. 2.3.2. Объединением множеств А и В называется множество С, которое состоит из всех элементов данных множеств А и В и только из них: С={х |хÎА или хÎВ}. Обозначается, А UВ.
Примеры. 1) A = {1; 2; 3}, B = {2; 3; 4; 5}, тогда C = A U B == {1; 2; 3; 4; 5}.
2) A = (–∞, 2], B = (1, +∞), тогда C = A U B = R.
3) А = [0; 7], В = [3; 10], тогда A U B = [0; 10].
3) Если А – множество студентов, не сдавших первый экзамен, В – второй, то А U В – множество студентов – задолжников после двух экзаменов (не исключено, что кто-то не сдал оба экзамена).
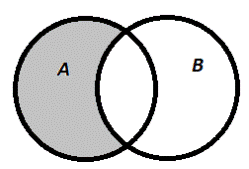
Опр.2.3.3. Разностью множеств А и В называется множество С, состоящее из всех элементов множества А, не принадлежащих множеству В: С={х | х Î А и х Ï В}. Обозначается, А\В.
Примеры 1) A = {1; 2; 3}, B = {2; 3; 4; 5}, тогда А\В={1}, В\А={4, 5}.
2) R \ Q – множество иррациональных чисел.
3) Q \ R = Æ.
Опр.2.3.4. Симметричной разностью множеств А и В называется множество С, состоящее из всех элементов множества А, не принадлежащих множеству В и всех элементов множества В, не принадлежащих множеству А: С={х | (х Î А и х Ï В) или (х Î В и х Ï А) }. Обозначается, А∆В.
Пример. А={1,2,3,4,5}, В={4,5,6,7}, А∆В= {1,2,3,6,7}
В каждом отдельном случае мы рассматриваем всевозможные подмножества одного и того же множества. Например, в начальной школе дети учатся работать (выполнять основные арифметические операции) сначала с числами из первого десятка натуральных чисел, затем из первой сотни и т.д. Но их действия не выходят за рамки натуральных чисел (отрицательные и дробные числа они будут проходить позже). Аналогично, учитель может работать с некоторыми группами учеников, которые будут являться подмножествами определенного множества обучаемых данным учителем школьников. Каждый человек носит различные комбинации вещей, но только из своего личного гардероба. Это основное множество (свое в каждом отдельном случае) называется универсальным множеством.
Опр.2.3.5. Универсальным множеством называется множество, подмножества которого (и только они) в данный момент рассматриваются. Обозначают, Е (или U в разной литературе).
При работе с числовыми множествами, если не дается дополнительных указаний, в качестве основного (универсального) множества будем считать множество R действительных чисел.
Опр.2.3.6. Дополнением множества А называется разность Е \А. Обозначается, А’ или  и читается «не-А». Иначе, дополнением множества А называется множество А’, состоящее из всех элементов, не принадлежащих множеству А.
и читается «не-А». Иначе, дополнением множества А называется множество А’, состоящее из всех элементов, не принадлежащих множеству А.
Примеры. 1) Е ={ множество студентов в группе}, A ={ множество студентов, сдавших первый экзамен}, то А’ ={ множество студентов, не сдавших первый экзамен}.
2) Е={буквы русского алфавита}, А={множество гласных букв}, тогда
А’={множество согласных букв и букв ь и ъ}.
3) Пусть Е – множество сотрудников школы, A – множество сотрудников старше 30 лет, B – множество сотрудников мужского пола, C – множество сотрудников занимающих должности вспомогательного персонала.
Тогда В ’ – множество женщин; А’ÇВÇC – множество мужчин занимающих должности вспомогательного персонала младше 30 лет; А È(В Ç С ’) – множество сотрудников старше 30 лет или мужчин не занимающих должности вспомогательного персонала; B \ C – множество мужчин, не являющихся вспомогательным персоналом; C \ B – множество сотрудников вспомогательного персонала – женщин.
4) Даны множества А={2, 3, 5, 8, 13, 15}, В={1, 3, 4, 8, 16}, С={12, 13, 15, 16}, D={0, 1, 20}. Найти АUВ, СUD, В∩С, А∩D, А\С, D\В, АUВUС, А∩В∩С, ВUD∩С, А∩С\D.
Решение: Будем пользоваться определениями соответствующих операций и учтем, что сначала должна выполняться операция пересечения множеств, а затем уже объединение или разность.
Получим АUВ={1, 2, 3, 4, 5, 8, 13, 15, 16};
СUD={0, 1, 12, 13, 15, 16, 20};
В∩С={16};
А∩D=Æ;
А\С={2, 3, 5, 8};
D\В={0, 20};
АUВUС={1, 2, 3,4, 5, 8, 12, 13, 15, 16};
А∩В∩С=Æ;
ВUD∩С={1, 3, 4, 8, 16};
А∩С\D={13, 15}.
5) Пусть Е={1, 2, 3, 4, 5, 6, 7, 8,9}, A={1, 2, 3, 5}, B={2, 4, 6, 8}, C={1, 3, 5, 7}, D={4, 5, 7, 8}. Выразить через заданные множества A, B, C, D следующие множества: 1) К={1,2,3,4,5,7,8}, 2) L={4, 7,8}, 3) F={2, 5}, 4) G={5, 7, 9}.
Решение: 1) K={1,2,3,4,5,7,8}=AUD.
2) L={4, 7,8}=D\A.
3) F={2, 5},
а) C\D={1, 3},
б) A\(C\D)={2, 5}.
4) G={5, 7, 9},
а) A∩D={5},
б) AUB={1, 2, 3, 4, 5, 6, 8},
в) (AUB)’={7, 9},
г) (A∩D)U((AUB)’)={5, 7, 9}.
Свойства операций над множествами:
Таблица 2.3.1.
| Свойства операции пересечения: 1) А∩А=А; 2) А∩Ø=Ø; 3) А∩А’= Ø; 4) А∩ Е =А; 5) А∩В=В∩А. | Свойства операции объединения: 1) АUА=А; 2) АU Ø =А; 3) АUА’= Е; 4) АU Е = Е; 5) АUВ=ВUА. |
| Свойства операции разности: | |
| 1) А\А=Ø; 2) А\ Ø =А; 3) А\А’= А; 4) А\ Е =Ø; | 5) Е \А=А’; 6) Ø \А=Ø; 7) А\В ≠ В\А. |
§ 2.4. Диаграммы Эйлера-Венна, таблицы вхождения элементов, координатная плоскость.
Для наглядного представления (графического изображения) множеств и результатов операций над ними удобно пользоваться так называемыми диаграммами Эйлера-Венна (кругами Эйлера).
При этом множества изображаются на плоскости в виде замкнутых кругов, а универсальное множество в виде прямоугольника. Элементы множества – точки внутри соответствующего круга.
Таблица 2.4.1.
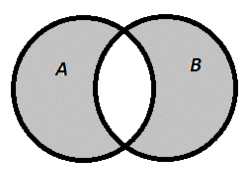
Объединение А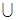 В: В:
| Пересечение А∩В:
| ||||||
Разность: А\В
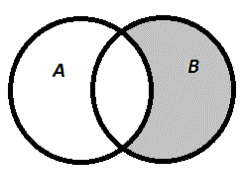
| Разность: В\А
| ||||||
Симметричная разность А∆В:
| Дополнение А’:

|
Примеры: Изобразить следующие множество с помощью диаграммы Венна
1) (АUВ)\(С∩А):
Таблица 2.4.2.
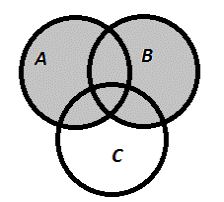
1)(АUВ)
| 2) (С∩А)
| ||||||
3) (АUВ)\(С∩А)

|
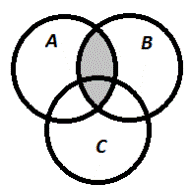
2) А∩В∩С;
а) А∩В
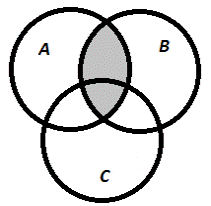
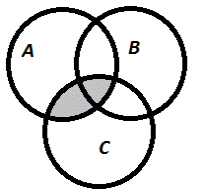
| б) А∩В∩С
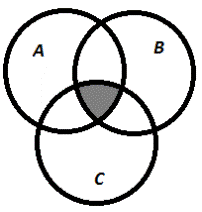
|
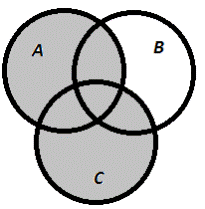
3) В\(АUС);
а) АUС
| б) В\(АUС)

|
4) (ВΔА)\С.
а) ВΔА
| б) (ВΔА)\С
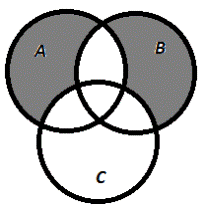
|
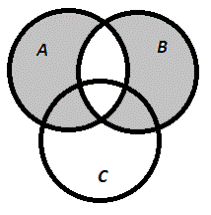
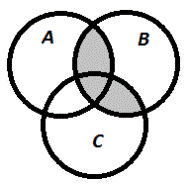
5) Выразить через множества А,В,С множество Е, которому соответствует заштрихованная область.

1. А∩В
| 2. В∩С
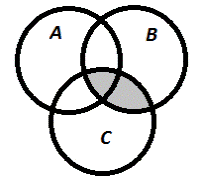
| 3.(А∩В)U(В∩С)
|
Есть и другой способ проиллюстрировать операции над множествами. Это, так называемая, таблица вхождения элементов в множества, в которой рассматриваются все возможные случаи вхождения выбранного элемента в множества А и В и их комбинации. Результат принадлежности этого элемента множествам А и В отмечают в первых двух столбцах таблицы по правилу: 1 – если элемент входит в данное множество, 0 – если не входит. Получится четыре случая или четыре строчки в таблице. Столбцы, соответствующие операциям A U B, A ∩ B, A \ B, заполняются согласно определений этих операций (табл. 1).
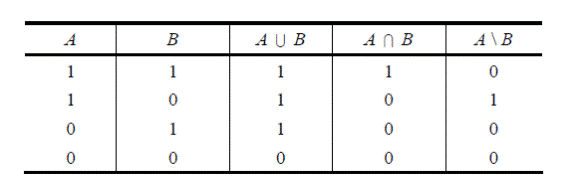
Например, вторая строка в табл. 1 читается так: если элемент входит в A, но не входит в B, то он входит в А U В, не входит в А ∩ В, но входит в A \ B.
Примеры. 1) С помощью таблицы вхождения элементов определите верно ли следующее равенство (А U В) ’ = А ’ ∩ В ’
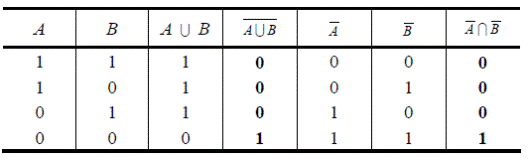
Из таблицы вхождения элементов в множества видно, что при различных вариантах вхождения элемента в множества А, В он входит или не входит в левую и правую части рассматриваемого равенства одновременно (см. четвертый и седьмой столбцы). Значит (А U В) ’ = А ’ ∩ В ’.
2) С помощью таблицы вхождения элементов определите верно ли следующее равенство (В U С) \ В = С.

Второй и четвертый столбцы не совпадают, поэтому это равенство неверное.
На координатной прямой множества изображаются в виде отрезка, концы которого показываются кружками: закрашенным кружком, если координата конца отрезка принадлежит множеству, в противном случае – не закрашенным кружком. Например, множество A = {x: − 2 < x ≤ 3} на координатной прямой можно показать так:
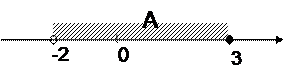
Примеры: Даны множества:
1) A = { x: − 5 ≤ x ≤ 6}, B = { x: − 3 < x < 8},
2) A = { х: −3 < х ≤ 2} и B = { х: 0 ≤ х < 5},
3) C = { х: 2 < х < 4} и D = { х: 3 ≤ х ≤ 5},
4) E = { х: −3 ≤ х ≤ 2} и F = { х: 2 < х ≤ 5}.
Найдите пересечения множеств и покажите их на координатной прямой.
Решение:
1)Изобразим на координатной прямой множества А и В:
 |
-3ÏВ, з начит, пересечению множеств А и В будут принадлежать все точки полуинтервала (-3, 6].
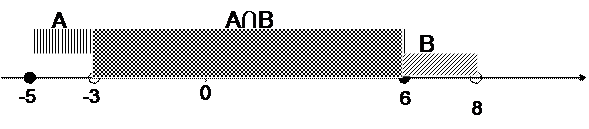 |
Зададим его с помощью характеристического свойства: A ∩ B = { х: -3 < х ≤ 6}.
2) Изобразим на координатной прямой данные множества:

 Множеству А и множеству В принадлежат все точки отрезка [0, 2]. Значит, пересечение множеств А и В можно изобразить на координатной прямой следующим образом:
Множеству А и множеству В принадлежат все точки отрезка [0, 2]. Значит, пересечение множеств А и В можно изобразить на координатной прямой следующим образом:
Зададим его с помощью характеристического свойства: A ∩ B = { х: 0 ≤ х ≤ 2}.
 3) Изобразим на координатной прямой множества C = { х: 2 < х < 4} и D = { х: 3 ≤ х ≤ 5}:
3) Изобразим на координатной прямой множества C = { х: 2 < х < 4} и D = { х: 3 ≤ х ≤ 5}:
4Ï C, з начит, пересечению множеств С и D будут принадлежать все точки полуинтервала [3, 4), точка 4 пересечению принадлежать не будет, т.е. C ∩ D = { х: 3 ≤ х < 4}.
 |
 4) Изобразим на координатной прямой множества E = { х: −3 ≤ х ≤ 2} и F = { х: 2 < х ≤ 5}:
4) Изобразим на координатной прямой множества E = { х: −3 ≤ х ≤ 2} и F = { х: 2 < х ≤ 5}:
Видим, что и 2Ï F, т.е. множества Е и F не имеют общих элементов, значит, E ∩ F = Æ.
5) G = { х: −3 ≤ х < 5} и S = { х: 3 ≤ х < 10}. На координатной прямой изобразить разность множеств G и S и разность множеств S и G.
Решение: Изобразим на координатной прямой множества G и S:
 |
Так как 3Î G и 3Î S, то 3Ï G \S. Значит, G\S= {-3≤ х <3}, S\G={5≤ х< 10}:
 |
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 25109; Нарушение авторских прав?; Мы поможем в написании вашей работы!