Теория устойчивости динамических систем

Метод (или математический аппарат), который используется в синергетике, - это теория динамических систем. Математический метод синергетики, то есть теория динамических систем, основан на дифференциальных уравнениях вида

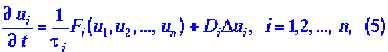
где 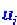- динамические переменные, например концентрация реагирующих веществ; 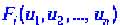- функции (в общем случае нелинейные), описывающие их (в смысле динамических переменных) взаимодействие в данной точке пространства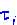; - характерные времена изменения переменных;
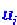Член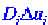 описывает распространение динамических переменных 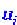в пространстве, в частности их диффузию ( 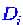- коэффициенты диффузии).

Уравнения (5) называют также уравнениями реакции с диффузией, поскольку они, в частности, описывают изменения концентрации веществ во времени и пространстве с учетом их диффузии и химических реакций. Принимают, что процессы, описываемые уравнениями (5), протекают в ограниченном пространстве - либо одномерном (реакции в трубке длиной L), либо двухмерном (реакции в пленке шириной порядка L), либо в трехмерном (реакции в сосуде, размеры которого порядка L).

В частном случае, когда все динамические переменные распределены в пространстве равномерно, мы имеем систему обыкновенных дифференциальных уравнений:

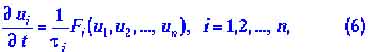
Последнее имеет место, если "длины диффузии"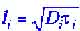 превышают пространственные размеры L системы. Уравнения (6), именуемые также точечными, хотя и проще уравнгений (5), тем не менее описывают многие неожиданные и интерсные явления.

Уравнения (5) и/или (6) являются динамическими, т.е. их решения, вообще говоря, однозначно определяются начальными и граничными условиями и, разумеется, свойствами и параметрами самих уравнений. Казалось бы, в такой ситуации ничего неожиданного быть не должно. Тем не менее характерные для синергетики неожиданности здесь возникают в случае, когда решения динамических уравнений теряют устойчивость. Обсудим это важное свойство.

Интуитивное представление об устойчивости (или неустойчивости) есть у каждого. Неустойчиво, например, состояние карандаша, поставленного на острие; неустойчиво движение шарика по гребню. В то же время движение его по ложбине устойчиво. Более точное представление дает анализ уравнений движения (и/или стационарных состояний). Этот анализ основан на исследовании поведения малых отклонений от соответствующего решения. Продемонстрируем это на примере стационарных состояний точечной системы. Стационарными являются состояния, соответствующие таким значениям переменных, при которых все функции равны нулю. При этом значения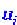 не меняются со временем, поскольку все производные также равны нулю. Однако малые отклонения от стационарных значений 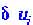меняются со временем, и их изменение можно описать системой линейных дифференциальных уравнений

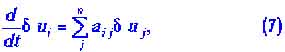
где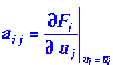

Решения имеют вид:

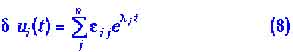
Здесь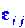 - коэффициенты, пропорциональные начальным отклонениям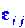,; они малы в меру малости последних.

Величины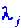 - числа, которые являются решениями алгебраического уравнения:

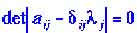
где		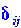-символ Кронекера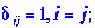

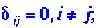
Величины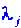 называются также числами Ляпунова и играют главную роль в анализе устойчивости.Если все числа Ляпунова отрицательны, то состояние устойчиво. Действительно, в этом случае все отклонения со временем уменьшаются, т.е. система стремится обратно к стационарному состоянию, даже если ее немного отклонить от него. Если хотя бы одно из чисел Ляпунова положительно, то состояние неустойчиво. Действительно, тогда отклонения 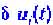возрастают со временем, причем достаточно быстро. Так в упомянутом примере - карандаш на острие - среди чисел Ляпунова имеются положительные по порядку величины равные. Это значит, что за время порядка 10 с начальные отклонения возрастут в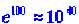 раз. Это колоссальная величина; она означает, что карандаш простоит на острие 10 секунд, только если начальные отклонения были бы меньше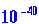см. Это абсурдно малая величина; фиксировать начальные условия с такой точностью, разумеется, невозможно.
В общем случае числа Ляпунова могут быть комплексными. Устойчивость определяется тогда знаком реальной части. Если среди чисел Ляпунова имеются равные нулю или чисто мнимые, то стационарное состояние называется нейтральным; при отклонении от него не появляются ни возвращающие, ни отклоняющие силы. Анализ неустойчивых движений основан на том же принципе: определяется временная зависимость малых отклонений от заданной траектории. Используются линейные по отклонениям уравнения (высшими степенями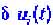 пренебрегают), решения которых имеют вид:

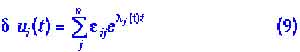
Числа Ляпунова при этом уже не постоянны, а зависят от времени. Траектория является неустойчивой, если среди чисел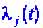 имеются такие, вещественные части которых положительны при.

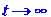Подчеркнем важное свойство: числа Ляпунова являются характеристическими (или собственными) числами системы; они не зависят от начальных условий. Таким образом, устойчивость (или неустойчивость) - внутреннее свойство исследуемой системы, а не результат внешнего воздействия. Особенность его в том, что проявляется оно только при наличии малых внешних воздействий.
Эта особенность привела к важным методологическим последствиям. Сейчас приходится пересматривать и подвергать ревизии некоторые, казалось бы, установившиеся в физике понятия.

Обсудим два примера.

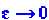Рассмотрим понятие абсолютно изолированной системы. Сейчас ясно, что его можно (и то не всегда) ввести лишь как предел неизолированной системы при стремлении к нулю величины внешнего воздействия. Для устойчивых систем такой предел существует и, следовательно, понятие остается в силе. В неустойчивых системах такой предел, вообще говоря, не существует. Действительно, предел величины, где, при и зависит от порядка стремления аргументов к своим пределам. Формально величину (которая отражает меру внешних воздействий) и время можно считать независимыми. Однако как мы уже убедились на конкретном примере, уже при сравнительно небольших временах экспоненциальный фактор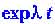 возрастает столь сильно, что компенсировать его уменьшением - задача абсурдная. Суть дела в том, что экспоненциальная зависимость (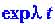) очень сильна, конкурировать с ней практически невозможно. Поэтому для неустойчивых систем понятие "абсолютно изолированная система" теряет смысл; можно лишь говорить об относительно изолированной системе.

Требует ревизии и понятие "причины". Обычно под причиной понимают начальные условия (или импульсные внешние воздействия), которые в соответствии с динамикой системы приводят к определенному результату - следствию. На этом языке слова "вскрыть причинно-следственные связи" означает "понять динамику промежуточных процессов". При этом негласно предполагают, что причины и следствия соизмеримы. Для устойчивых (или нейтральных) процессов это всегда имеет место. В неустойчивых процессах ситуация иная: очень малая причина приводит к следствию, которое по масштабам с причиной несоизмеримо. Обычно в таких случаях говорят, что причиной явилась неустойчивость, а не малое начальное воздействие. При этом, однако, происходит весьма существенный сдвиг понятий: в качестве причины фигурирует внутреннее свойство системы, а не внешнее воздействие.

Поясним сказанное на житейском примере. Рассмотрим два случая. В первом хрустальная ваза стоит на середине стола (состояние устойчиво). Прошел некто и неловким движением толкнул вазу со стола - она разбилась. В чем причина столь печального события, или, другими словами, кто виноват? Понятно, что виноват "некто", а причина - его неловкие движения.

Рассмотрим другой случай: ваза стоит на краю стола, так что чуть-чуть не падает (состояние, близкое к неустойчивому). Пролетела муха - ваза разбилась. В этом случае муху не обвиняют, а говорят, что причина событий в неустойчивом положении вазы. Виноват тот, кто ее поставил (так, чтобы никто не был виноват, в жизни обычно не бывает).

Забегая несколько вперед, отметим, что в основе утверждения "событие произошло случайно" (т.е. без видимой причины) также лежит неустойчивость динамических систем.

Дата добавления: 2014-01-07