
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Динамический хаос
|
|
|
|
Один из самых интересных и важных разделов синергетики - так называемый динамический хаос. Как в рамках чисто динамической системы возникает хаотический режим с непредсказуемым поведением?
Вопрос это возник сравнительно давно, и история его не лишена драматизма. Людвиг Больцман поставил себе целью "вывести" законы термодинамики, в частности закон возрастания энтропии, из законов классической механики. В качестве модели идеального газа он рассмотрел систему из многих шаров (число шаров N>>1), которые двигаются и упруго сталкиваются друг с другом. Эта модель получила название "задача о бильярде". С точки зрения синергетики эта модель - динамическая система, содержащая 6N переменных (координаты и скорости всех шаров в трехмерном пространстве). Соответственно фазовое пространство системы многомерно, т.е. содержит 6N измерений. Полная энергия системы сохраняется (как и полагается в классической механике), т.е. система консервативна. Это значит, что соударения абсолютно упругие и "трение" на участках между соударениями отсутствует, поскольку молекулы (т.е. шары) летят в вакууме.
Поставленную задачу Больцман решил, т.е. вывел так называемую H-теорему, продемонстрировал необратимое возрастание энтропии и выяснил микроскопический смысл самого понятия энтропии. Именно он показал, что энтропия пропорциональна логарифму вероятности застать систему в определенном состоянии (в котором положения и скорости всех шаров фиксированы). В процессе вычислений Больцман использовал гипотезу о том, что изображающая точка, двигаясь по фазовой траектории, равномерно заполняет все доступное фазовое пространство.
Гипотеза получила название молекулярного хаоса, она казалась вполне естественной, хотя в то время и не была обоснована. Результаты Больцмана вошли в науку как замечательное достижение человеческого разума. Тем не менее триумф Больцмана был омрачен. Его коллега и друг математик Цермело сказал, что Больцман в расчетах где-то допустил ошибку. Действительно, исходная система уравнений, которую использовал Больцман, консервативна и обратима во времени (как и любая механическая система без трения), в то время как конечный результат - возрастание энтропии - явно необратим. Следовательно, где-то в расчетах нарушена симметрия исходных положений (в данном случае симметрия относительно обращения времени); нарушать симметрию нельзя (во всяком случае без веских причин). Больцман не смог ответить Цермело и застрелился.
Следующим был замечательный физик Эренфест. Он взялся за решение задачи и сформулировал проблему максимально четко, но решить ее не смог и застрелился. Ответ был дан (точнее, сформулирована основная идея ответа) только в 1948 году молодым физиком Н.С.Крыловым. Главная идея сводилась к следующему: симметрия в динамических системах может нарушаться и молекулярный хаос может возникать, если динамические решения неустойчивы. Сформулировав эту идею Н.С.Крылов скончался.
Последовательная математическая теория была развита в работах школы Колмогорова Д.В.Амосовым и Я.Г.Синаем. Было показано, что в задаче о бильярде любая траектория системы неустойчива, т.е. фазовое пространство сплошь состоит из сепаратрис[1]), а устойчивых состояний вообще нет.
Продемонстрируем этот эффект.
Соударение двух шаров радиуса r можно свести к задаче об отображении точки от выпуклой поверхности радиуса 2r. Пусть до соударения траектории были отклонены друг от друга на малый угол. После соударения угол становится существенно больше. Его легко вычислить, используя закон упругого отражения и элементарную геометрию:

| ||
| где |  длинна пробега между соударениями длинна пробега между соударениями
| 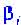 -угол удара -угол удара
|
Отсюда видно, что при каждом соударении угол отклонения возрастает и после n-го удара будет равен

|
Число соударений n растет со временем , где
, где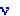 - частота соударений. Поэтому формулу (9) можно представить в в виде:
- частота соударений. Поэтому формулу (9) можно представить в в виде:

| |
| здесь | 
|
черта сверху означает усреднение по данной траектории.
Величина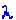 является числом Ляпунова; она положительна, и следовательно, отражение от выпуклой поверхности неустойчиво.
является числом Ляпунова; она положительна, и следовательно, отражение от выпуклой поверхности неустойчиво.
Сделаем ряд замечаний.
Сказанное относится к любой траектории независимо от начальных условий. Это значит, что неустойчива любая траектория, или, другими словами, в задаче о бильярде любая траектория может считаться сепаратрисой. Здесь мы имеем дело с неустойчивостью особого типа - глобальной неустойчивостью.
Число шаров в задаче существенной роли не играет. Глобальная неустойчивость имеет место даже когда существует всего один шар в плоском бильярде, если хотя бы одна из стенок его выпукла внутрь. Такая система и называется бильярдом Синая. В этой задаче фазовое пространство имеет четыре измерения (две координаты и две скорости). Траектория шара в обычном понимании в этом случае представляет собой проекцию фазовой траектории изображающей точки на обычное пространство.
Глобальная неустойчивость приводит к тому, что поведение системы становится хаотическим и все доступное фазовое пространство заполняется равномерно. Такие системы по предложению Колмогорова называют перемешивающимися (или К-системами). В них приобретает новый смысл понятие энтропии как меры неустойчивости. Симметрия по отношению к обращению времени в таких системах нарушается, и возникает необратимость опять таки в связи с глобальной неустойчивостью.
В задаче о бильярде радиус взаимодействия имеет четкий смысл - это удвоенный радиус шаров r. Если расстояние между центрами шаров больше 2r - силы отсутствуют, если расстояние меньше - сила бесконечна. В реальных молекулах зависимость силы взаимодействия более плавная. Тем не менее можно ввести "эффективный радиус", если сила обратно пропорциональна, например, кубу расстояния (или зависит от него еще более резко). В этом случае можно считать, что в формуле (21) r - эффективный радиус. В случае, когда сила обратно пропорциональна квадрату расстояния, эффективный радиус формально оказывается бесконечным. Говорят, что такие силы дальнодействующие. Именно таковы силы гравитационного и электростатического взаимодействия.
Полагая, что в формуле (21)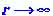 , видим, что
, видим, что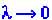 . Это значит, что при дальнодействующих силах глобальная неустойчивость отсутствует, даже если число взаимодействующих объектов в системе велико. Этот вывод очень важен; действительно, число объектов, например в Солнечной системе достаточно велико: это планеты, их спутники и т.д. Однако благодаря дальнодействию эти объекты не сталкиваются и движутся по вполне определенным траекториям. Глобальной неустойчивости и хаоса в этой системе нет, что и позволяет нам жить относительно спокойно.
. Это значит, что при дальнодействующих силах глобальная неустойчивость отсутствует, даже если число взаимодействующих объектов в системе велико. Этот вывод очень важен; действительно, число объектов, например в Солнечной системе достаточно велико: это планеты, их спутники и т.д. Однако благодаря дальнодействию эти объекты не сталкиваются и движутся по вполне определенным траекториям. Глобальной неустойчивости и хаоса в этой системе нет, что и позволяет нам жить относительно спокойно.
Таким образом, для возникновения молекулярного хаоса необходимым и достаточным условием является глобальная неустойчивость. Большое число частиц не является ни необходимым, ни достаточным условием; это следует подчеркнуть, поскольку до недавнего времени (да и сейчас) в солидных книгах часто утверждалось обратное. Сейчас Больцман мог бы ответить Цермело вполне обоснованно и указать не только "причину" молекулярного хаоса, но и очертить область применимости этой гипотезы, в частности привести примеры, в которых она не реализуется.
Теория динамического хаоса имеет также и методологическое значение. Ранее многие полагали, что молекулярный хаос - удобная форма описания, когда мы не знаем или не можем вычислить истинных траекторий. При этом неявно предполагалось, что вот уже поднатужимся и сможем предсказать.
ЗАКЛЮЧЕНИЕ
Атом - член такой малой системы, как молекула; молекула входит в системы другого порядка величины: каплю, атмосферу. Такое прогрессивное возрастание порядка величины систем возможно только при "переплетении силовых отношений". Гартман формулирует следующий основной закон ступенчатости природы: внешние силы меньших систем являются одновременно внутренними силами больших систем (по существу их "строительным моментом"). Например, характерная внешняя сила атомов - химическое сродство - является внутренней силой для систем большего порядка величины - молекул, в которых объединяются, связываются атомы. Система, в которой внешние силы ее элементов не были бы гармонично включены в целое, не являлась бы стабильной. Динамический закон ступенчатости природы может быть сформулирован как закон селекции систем: из меньших систем возникают только такие большие системы, в которых внешние силы их элементов (меньших систем) являются одновременно их внутренними силами.
Этот закон, казалось бы, предполагает, что "природа построена снизу", т. е. сначала возникают меньшие системы, а потом из них большие.. Однако фактически это не так. Закон допускает и такую формулировку: из больших систем могут образоваться только такие меньшие системы, внешние силы которых являются внутренними силами больших систем.
Устойчивость динамических систем имеет свой характер, чем устойчивость субстанции. Сущность их устойчивости в перевесе внутренних сил над внешними. Даже внешняя форма этих образований определяется их внутренним сопротивлением внешним воздействиям и сохраняется, несмотря на деформирующие влияния. Динамическая система разрушается только тогда, когда освобождаются внутренние силы (например, спонтанный распад атома путем излучения) или когда внешние силы превосходят внутренние силы (разрушение комет, химические реакции и т. д.).
Стабильность динамических систем, таким образом - функция и внутренних, и внешних сил. Существует закон обратной зависимости между величиной и "силой" (в смысле устойчивости) динамических систем. Самые "сильные" из известных нам образований - атомные ядра, т. е. системы наименьшего масштаба. Атомное ядро "сильнее", чем атом (связь в атоме); связь в атоме "сильнее" чем связь в молекуле; простые молекулы "сильнее", чем сложные органические молекулы и составленные из них тела.
Итак, сохранение динамических систем происходит не на основе "инертного" постоянства вещества или энергии, а на основе динамического подвижного равновесия, внутреннего "выравнивания" процессов и сил, саморегуляции, хотя и автоматической. "Эти формы равновесия, - пишет Гартман в 1947 г. в работе «Цели и пути категориального анализа", являются основным категориальным моментом, имеющим силу для всех высших форм систем (вплоть до общественных). Конечно, при этом формы равновесия выступают в таком измененном виде, что их трудно бывает распознать"
ЛИТЕРАТУРА
1. Барбашин Е.А. Функции Ляпунова. М.: Наука, 1970. 240 с.
2. Барбашин Е.А. Введение в теорию устойчивости. М.: Наука, 1967. 215 с.
3. Демидович Б.П. Лекции по математической теории устойчивости. -М.:Наука, 1967. 472 с.
4. Малкин И.Г. Теория устойчивости движения. М.; Л.: Гостехиздат, 1952. 432 с.
5. Руш Н., Абетс П., Лалуа М. Прямой метод Ляпунова в теории устойчивости. М.: Мир, 1980. 304 с.
6. Тихомиров О.Г. Устойчивость однородных нестационарных систем обыкновенных дифференциальных уравнений // СПб.: Вестник СПбГУ. Сер. 10, вып. 3. 2007. С. 123 130.
КАЧЕСТВЕННОЕ ИССЛЕДОВАНИЕ
МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 1903; Нарушение авторских прав?; Мы поможем в написании вашей работы!