Модели — две категории вопросов

Какого рода вопросы ставятся при исследовании моделей, заданных системами дифференциальных уравнений? Зная значения параметров, мы можем для любых начальных значений фазовых переменных решить (как правило, численно на ЭВМ) систему дифференциальных уравнений и предсказать ход процесса во времени, т. е. рассчитать поведение интересующих нас переменных во времени: x(t), y(t) и т. д.

Решения системы дифференциальных уравнений удобно представлять в виде траекторий — кривых, вычерчиваемых изображающей точкой (x(t), y(t),...) в пространстве фазовых переменных (х, у,...) с течением времени t. В случае системы с двумя фазовыми переменными траектория — это гладкая кривая на фазовой плоскости.

Замечание. Траектории, отвечающие различным начальным условиям, не пересекаются (либо целиком совпадают). Все множество различных траекторий целиком заполняет фазовую плоскость.

Математические модели, подобные описанным в предыдущем параграфе, относятся к разряду качественных: они

призваны описывать принципиальные, качественные свойства изучаемых процессов, а не их детальные характеристики. При заведомой количественной неточности моделей точное их решение имеет мало смысла. Возникающие при исследовании таких моделей вопросы должны носить качественный характер. Впрочем, вопросы качественного характера, как правило, оказываются интересными, даже когда имеется точное описание моделируемого процесса.

Таким образом, интерес представляет не отдельная реализация процесса (отдельная траектория), а поведение системы в целом, т. е. совокупность реализаций (совокупность траекторий) и зависимость общих свойств этой совокупности от параметров модели. Качественные вопросы естественно разделить на две категории.

Вопросы первого типа относятся к поведению системы при фиксированных значениях параметров. Самым существенным при этом является качественное понимание характера режимов, устанавливающихся в системе по прошествии достаточно большого времени (как говорят, по завершении переходного процесса). Вообще говоря, в системе в зависимости от начальных усло­вий могут устанавливаться различные режимы: в химическом реакторе при различных начальных концентрациях веществ реакция может либо прекратиться, либо может установиться неко­торая постоянная скорость реакции (иногда одна из нескольких возможных); реакция может идти в пульсирующем режиме; наконец, реактор может разрушиться. Сходным образом взаимодей­ствие болезнетворных микроорганизмов (или злокачественных клеток) и иммун­ных клеток может привести к гибели организма, к его излечению, к переходу болезни в хроническую форму или в режим периодических обострений. Вопросы первого типа как раз и подра­зумевают предсказание того, какие режимы могут устанавливаться в данной системе при фиксированных значениях параметров.

Ответы на вопросы первого типа можно получить из так называемого фазового портрета системы — совокупности всех ее траекторий, изображенных в пространстве фазовых перемен­ных (фазовом пространстве). Среди этих траекторий имеется некоторое число ос­новных, которые и определяют качественные свойства системы. К ним относятся прежде всего точки равновесия, отвечающие стационарным режимам системы, и замкнутые траектории (циклы), отвечающие режимам периодических колебаний. Будет ли режим устойчив или нет, можно установить по поведению соседних траекторий: устойчивое равновесие или цикл притягивает все близкие траектории, неустойчивое отталкивает хотя бы некоторые из них. Наконец, в свете сформулированных вопро­сов интерес представляют области притяжения различных устойчивых режимов и границы этих областей.

Вопросы второго типа касаются событий, происходящих в системах при изменении значений параметров. Постепенное изменение параметра, например температуры Т в химической системе, может приводить к тому, что при пе­ресечении некоторого критического значения установившийся в системе режим претерпевает качественное изменение. Например, ранее стационарный ход реакции сменяется пульсирующим режимом. Изменение другого параметра, например парциального давления р одного из газов в реакционной смеси, может приводить к другому качественному изменению хода установившегося процесса, например к скачкообразному изменению скорости течения процесса.

При таких перестройках, очевидно, меняется фазовый портрет изучаемой системы. Качественные перестройки фазового портрета называются бифуркациями. Вопросы второго типа, следовательно, подразумевают определение бифуркационных (критических) значений параметров и описание явлений, происходящих при переходе через кри­тические значения. Таким образом, возникает задача разбиения пространства параметров системы на области с качественно различными типами динамического поведения — построение параметрического портрета системы. Построенный параметрический портрет в совокупности с соответствующими фазовыми портретами содержит в концентрированном виде информацию о возможных в системе динамических режимах и их качественных перестройках. Следующие параграфы этой главы содержат предварительное обсуждение математических понятий, возникающих при постановке вопросов качественного характера. Основное внимание уделяется системам двух дифференциальных уравнений — случаю, для которого имеется наиболее полная, далеко продвинутая и геометрически наглядная мате­матическая теория. Заметим, что результаты, полученные в рамках этой теории, обладают большой степенью общности и применимы к системам более высокой размерности

4. Качественная теория и теория бифуркаций

Математическое изучение вопросов качественного характера, тип которых указан выше, составляет предмет ка­чественной теории и теории бифуркаций динамических систем. Основы этих математических дисциплин были заложе­ны в конце прошлого и первой поло­вине нынешнего столетия в трудах А. М. Ляпунова, А, Пуанкаре, А. А. Андронова и др.

Вопрос о качественном исследовании системы дифференциальных уравнений при фиксированных значениях параметров ставится в качественной теории следующим образом. Автономная система дифференциальных уравнений оп­ределяет разбиение фазового пространства на траектории — фазовый портрет системы. Требуется установить топологическую (качественную) структуру фазового портрета, т. е. такой набор его свойств, которые сохраняются при непрерывной деформации фазового портрета.

Рассмотрим более подробно качественную структуру фазового портрета системы двух дифференциальных уравнений (системы на плоскости). Эта структура определяется типом и взаимным расположением положений равновесия, предельных циклов и сепаратрис. Положение равновесия — это точка фазовой плоскости, в которой обращаются в нуль правые части системы. Положения равновесия отвечают стационарным режимам. Под типом положения равновесия понимается структура фазового портрета в его малой окрестности. Существуют три «основных» типа положений равновесия: устойчивый узел (или фокус), неустойчивый узел (или фокус), седло. Фазовые портреты для этих положений равновесия изображены далее на (рис. 4.1).

Устойчивый узел (фокус) притягивает все близкие траектории (т. е. любые малые возмущения затухают). Такое положение равновесия отвечает установившемуся стационарному режиму. Неустойчивый узел (фокус), наоборот, отталкивает все близкие траектории (если обратить знак времени, то отталкивание заменяется притяжением). Положение равновесия типа седло принципиально отличается от указанных двух типов равновесий. Имеются ровно две траектории, которые притягиваются к седлу и называются входящими сепаратрисами, и две траектории, «выходящие» из седла, — выходящие сепаратрисы. Все остальные траектории могут подходить сколь угодно близко к седлу, но затем с течением времени будут удаляться от него (поло­жение равновесия типа седло неустойчиво).

Предельный цикл — это замкнутая траектория на фазовой плоскости. Пре­дельные циклы отвечают режимам периодических колебаний. Тип предельного цикла — это также топологическая структура фазового портрета в его окрестности. Для системы на плоскости различают два основных типа предельных циклов: устойчивый и неустойчивый. В первом случае все близкие траектории стремятся к предельному циклу, «накручиваясь» на него, во втором удаляются от предельного цикла, «скручиваясь» с него. Устойчивый предельный цикл соответствует режиму автоколебаний.

Замечание. Тип положения равновесия можно определить, вычислив некоторые два (действительных или комплексных) числа, называемых собственными числами положения равновесия (это собственные числа матрицы линеаризации системы в положении равновесия, или, что то же самое, корни характеристического уравнения). Тип предельного цикла определяется одним числом — мультипликатором цикла. Все эти числа характеризуют скорости экспоненциального роста или затухания возмущений стационарного и колебательного режимов.

Пример фазового портрета системы на плоскости представлен на рис. 1.1. Это один из фазовых портретов эко­логической системы (1.2). На нем име­ются положения равновесия всех основ­ных типов и устойчивый предельный цикл. Фазовый портрет показывает, что при положительных начальных численностях популяций хищника и жертвы в системе может устанавливаться один из двух возможных режимов: либо режим автоколебаний, отвечающий предельному циклу Г, либо стационарный режим, отвечающий положению равновесия 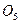Области начальных значений, из которых устанавливается тот или иной режим, разделены линией, образованной входящими сепаратрисами седла 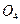. Отметим, что границами областей притяжения в системе на плоскости, кроме входящих сепаратрис седел, могут служить и неустойчивые предельные циклы.

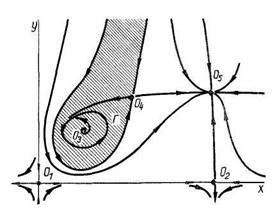
Рис 1 1 Фазовый портрет экологической модели (1 2) для некоторого набора значений параметров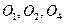— положения равновесия типа седло, 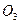— неустойчивый фокус, 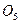— устойчивый узел Заштрихована область притяжения устойчивого предельного цикла G, т е область начальных значений, отвечающих установлению режима автоколебаний

Полученные из исследования фазового портрета качественные выводы могут быть весьма существенны для предсказания поведения и управления экосистемой. Пусть, например, жертвы в модели (1.2) — это жуки, являющиеся вредителями леса, а хищники — поедающие этих жуков птицы. Пусть далее автоколебательному режиму, связанному с циклом Г, отвечают относительно низкие численности вредителей, а стационарному состоянию О₅ — высокие чис­ленности вредителей. Фазовый портрет (рис. 1.1) показывает, что полезные на первый взгляд внешние воздействия на экосистему (например, применение инсектицидов), приводящие к массовой гибели вредителей, могут давать затем неожиданные последствия — вспышку их численности. Действительно, если система исходно находилась в режиме автоколебаний и воздействие было таково, что вывело изображающую точку за пределы заштрихованной области (области притяжения цикла Г), то в системе установится стационарный режим О₅, отвечающий большей численности вредителей.

Одним из основных понятий качественной теории является понятие грубой (структурно устойчивой) системы, введенное А.А.Андроновым и Л. С. Понтрягиным (1937). Это понятие формализует следующее наблюдение: топологическая структура фазового портрета, как правило, не меняется при малом изменении системы (в частности, при малом изменении ее параметров). Свойство сохранения структуры фазового портрета при малых возмущениях системы было взято в качестве определения грубости и затем было доказано, что почти всякая система на плоскости является грубой.

Замечание. Говоря об основных типах положений равновесия и предельных циклов, мы имели в виду именно грубый случай. В грубой системе собственные числа положений равновесия не лежат на мнимой оси, а мультипликатор цикла не равен единице.

Если менять параметры грубой системы, то ее фазовый портрет будет также меняться, но его топологическая

структура в некотором диапазоне значений параметров будет оставаться постоянной. При достижении критических значений параметров происходит бифуркация — меняется топологическая структура фазового портрета. Задача качественного исследования системы, зависящей от параметров, состоит в том, чтобы описать все возможные в ней бифуркации, построить множество бифуркационных значений параметров, разбивающее пространство параметров на области с различными типами (грубых) фазовых портретов, и указать для каждой области соответствующий ей фазовый портрет. Полученное в результате такого бифуркационного исследования разбиение пространства параметров и есть параметрический портрет системы.

Пример параметрического портрета и набора соответствующих фазовых портретов для обсуждавшейся выше эколо­гической модели (1.2) представлен далее в (рис. 4.24).

Дата добавления: 2014-01-07