Волновая функция

Состояние микрочастицы (характеристики её движения, взаимодействия с другими частицами и т.д.) полностью задаётся функцией, которую называют волновой функцией и обозначают Y (пси-функция).

Принцип суперпозиции состояний. Если частица может находиться в одном состоянии и может находиться в другом состоянии, то она может находиться и в состоянии, являющимся суперпозицией этих состояний. Это означает, что если первое состояние описывается волновой функцией Y₁, а второе Y₂, то состояние, являющееся суперпозицией состояний, описывается волновой функцией, являющейся их линейной комбинацией: Y₃= с ₁Y₁+ с ₂Y₂, где с ₁ и с ₂ – некоторые константы.

Суперпозиция состояний в квантовой механике отличается от суперпозиции состояний в классической физике. Например, в классической физике суперпозиция колебаний приводит к новому колебанию с большей или меньшей амплитудой. Возможен даже случай нулевой амплитуды. В квантовой механике же нулевая амплитуда соответствует отсутствию частицы в данном состоянии.

Для того чтобы определить какую-то физическую величину, описывающую состояние частицы, надо осуществить некие математические операции над волновой функцией, соответствующей данному состоянию, и проанализировать полученные результаты.

Процесс определения значения какой-то физической величины А в соответствующем состоянии частицы, по своей сути является процессом измерения данной физической величины, меняющим состояние частицы. Поэтому в результате измерения должна измениться волновая функция данного состояния. Таким образом, процесс измерения следует описывать правилом, по которому меняется волновая функция, т.е. следует задать соответствующую «функцию от функции» или оператор физической величины 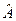, сопоставляющий волновой функции одного состояния Y волновую функцию другого состояния 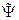. Математически процесс измерения можно записать так . Принцип суперпозиции требует, чтобы этот оператор был линейным, т.е. .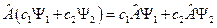

Допустим, что при измерении некоторой физической величины в состоянии с волновой функцией Y₁ получается одно значение А ₁, а в состоянии с Y₂ – другое А ₂. Какое значение получится при измерении физической величины в состоянии, являющимся суперпозицией этих состояний: Y₃=с₁Y₁+с₂Y₂?

Процесс измерения любой физической величины носит вероятностный характер. Т.е. тот или иной результат измерения можно получить с какой-то определённой вероятностью. Это означает, что при однократных измерениях мы будем получать значения А ₁ или А ₂ с некоторыми, вообще говоря, разными вероятностями р ₁ и р ₂.

Замечание. Состояние, в котором при однократных измерениях физических величин всегда получаются одни и те же значения, принято называть чистым состоянием. В обратном случае, состояние называют смешанным.

Требования, чтобы измерения сводились к операциям над волновыми функциями, приводят к условию, налагаемому на математическое выражение для волновой функции: она должна быть функцией, принимающей значения в комплексном пространстве. Поэтому для неё справедливы все операции над комплексными числами.

Дата добавления: 2014-01-07