Математическое отступление

Напомним, что символом 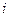обозначается такое комплексное число, что .

Любое комплексное число z может представлено в виде 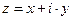, где x и y – вещественные числа. При этом число x называется вещественной частью числа z и обозначается 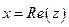, а число y называется мнимой частью числа z и обозначается .

Число z * является комплексно сопряжённым числу 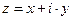, если .

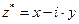В частности . Для вещественного числа .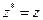

Сумма двух комплексных чисел 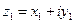и 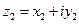равна: .

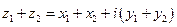Произведение двух комплексных чисел 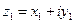и 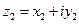равно:

и не зависит от порядка сомножителей.

В частности, .

Величина 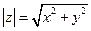называется модулем комплексного числа .

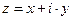Т.е. 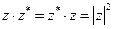. Кроме того, .

Для того чтобы разделить одно комплексное число 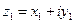на другое 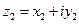надо знаменатель и числитель дроби умножить на комплексно сопряжённое число к знаменателю:

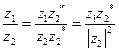. В частности, .

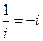Для числа 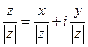можно записать: .

Следовательно, существует такой угол j, что 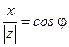, 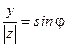. Тогда комплексное число 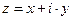можно записать в виде .

Соотношение Эйлера можно получить следующим образом. Обозначим . Тогда справедливо соотношение

.

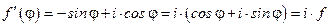Решением этого дифференциального уравнения, с учётом условия 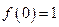, является функция 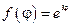, поэтому . Это соотношение позволяет привести ещё более короткую запись для комплексного числа .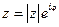

С учётом такой формы записи получаем, что , , .

.

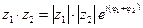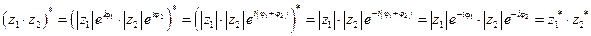Возведение комплексного числа в степень.

Извлечение корня n -й степени 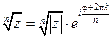(где k =0,, n -1) даёт n корней.

Замечание. .

Статистический смысл волновой функции.

Макс Борн предложил следующий смысл волновой функции.

dP - вероятность того, что частица находится в некоторой малой области пространства, объём которой dV, определяется равенством

т.е. квадрат модуля волновой функции равен плотности вероятности нахождения частицы в некоторой области пространства . Поэтому для нахождения вероятности того, что частица находится в некоторой области V надо вычислить интеграл .

Следовательно, если частица не может находиться в области V, то .

Т.к. , то это равенство возможно при , т.е. 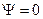в этой области V.

Если частица обязательно находится в области V, то .

Следовательно, квадрат модуля волновой функции должен быть интегрируемой функцией по этой области.

Замечание. Вероятность того, что частица находится в какой-то определённой точке, равна нулю, т.к. в этом случае объем соответствующей области нулевой.

Уравнение Шрёдингера.

Волновая функция должна являться решением уравнения Шрёдингера:

,

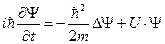где m – масса частицы, , U – действительная функция координат и времени, такая, что вектор 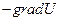является классическим аналогом силы, действующей на частицу. В случае, когда U не зависит от времени, она совпадает с потенциальной энергией.

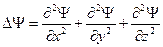- результат действия на функцию Y оператора Лапласа.

Следовательно, волновая функция должна быть непрерывно-дифференцируемой один раз по времени и два раза по пространственным координатам.

Уравнение 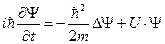носит название (временного) уравнения Шрёдингера (по имени немецкого физика Эрвина Шрёдингера, предложившего его в 1926 году).

Уравнение Шрёдингера является одним из постулатов (аксиом) квантовой механики и играет в квантовой физике такую же фундаментальную роль, как уравнения Ньютона в классической механике и уравнения Максвелла в классической электродинамике.

Уравнение Шрёдингера является линейным, т.е. линейная комбинация решений тоже является решением. Действительно, если каждая из функций Y₁ и Y₂ является решением, то их линейная комбинация Y₃= с ₁Y₁+ с ₂Y₂ (где с ₁ и с ₂ – некоторые константы) тоже является решением, т.к. уравнение в силу равенств

или

является линейной комбинацией уравнени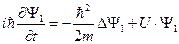й

и .

Следовательно, принцип суперпозиции состояний не противоречит уравнению Шрёдингера.

Замечание. Сопряжённое уравнение Шрёдингера для волновой функции имеет вид

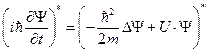или .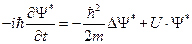

Пример. Найдем волновую функцию для свободно движущейся частицы в одномерной области (волны де Бройля). В этом случае U =0, поэтому уравнение Шрёдингера принимает вид

.

Пусть частица движется вдоль оси Х, тогда получаем соотношение .

Решение этого уравнения ищем в виде плоской волны (С = const)

.

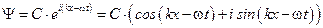После подстановки в уравнение выражений для производных

,

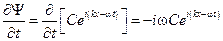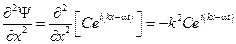
получаем равенство .

После сокращений остаётся . Если по аналогии с фотоном свободной частице приписать энергию 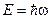и импульс 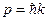, то получим классическое соотношение между кинетической энергией и импульсом .

Рассмотрим решение типа плоской волны для частицы, которая движется в одномерной области, в которой U (x) не зависит от времени. Т.к. в этом случае и уравнение Шрёдингера имеет вид 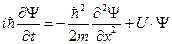, то после подстановки функции в уравнение получаем равенство

.

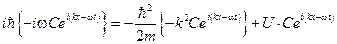Получаем соотношение 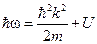, которое можно трактовать как определение механической энергии в классической физике .§

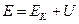Замечание. Для свободной частицы квадрат модуля волновой функции равен

.

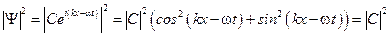Поэтому интеграл имеет смысл только для ограниченной области.

Условие нормировки.

Уравнение Шрёдингера линейное, поэтому если решением является функция Y, то решением является также и функция 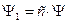, где с = const. В этом смысле говорят, что волновая функция определяется с точностью до константы.

Из физического смысла следует, что для всей области определения волновой функции V справедливо утверждение – вероятность того, что частица находится в этой области V, равна единице

.

Следовательно, если при решении задачи о поиске волновой функции в некоторой области было найдено решение Y₁, но при этом 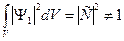, то в качестве волновой функции следует взять функцию 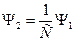, т.к. она тоже является решением и для неё выполняется

.

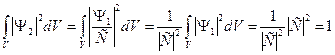Правило выбора решения Y, такого, что для него во всей области выполняется условие

называется условием нормировки решения на единицу или просто условием нормировки.

Замечание. В принципе, формально можно выбрать и другое условие нормировки – например:

,

но тогда квадрат модуля волновой функции уже не будет иметь смысл плотности вероятности.

Вектор плотности потока вероятности.

В классической физике из уравнений движения частиц или уравнений Максвелла следуют разнообразные законы сохранения и уравнения непрерывности. Посмотрим, как обстоит дело с уравнением Шрёдингера.

Если частица не находится постоянно в некоторой области пространства V, то вероятность её нахождения в этой области должна зависеть от времени. Поэтому в этом случае

.

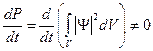Предполагаем, что объём неподвижен, поэтому

.

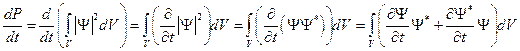Из уравнения Шрёдингера следует, что

.

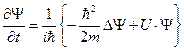Из сопряжённого уравнения Шрёдингера

.

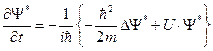Тогда

откуда после сокращений

.

Т.к. 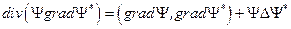и , то

.

С учётом теоремы Остроградского-Гаусса получаем

.

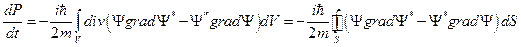Вектор плотности вероятности определяется соотношением

.

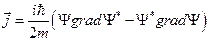Уравнение непрерывности для вероятности в интегральной форме:

изменение вероятности нахождения частицы в некотором объёме V равно с обратным знаком потоку вектора плотности вероятности через замкнутую поверхность S, ограничивающую этот объём.

Т.к. для неподвижного объёма справедливо равенство 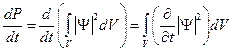, то из равенства можно получить

уравнение непрерывности для вероятности в дифференциальной форме:

.

Стационарные состояния.

Состояния частицы, для которых значение энергии определено однозначно, называются стационарными состояниями.

Замечание. Из принципа неопределённостей для времени и энергии 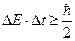следует, что если неопределённость энергии в каком-то состоянии стремится к нулю 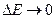, то время пребывания системы в этом состоянии должно быть бесконечно большим. В этом смысле состояние называется стационарным.

Как будет установлено далее (в теории операторов), волновая функции частицы в стационарном состоянии со значением энергии Е принимает особый вид

,

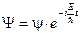где функция «пси малая» y зависит только от координат частицы, но не зависит от времени, поэтому её иногда называют координатной частью волновой функции стационарного состояния.

В стационарном состоянии плотность вероятности не зависит от времени. Действительно, плотность вероятности равна квадрату модуля волновой функции

.

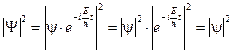Следовательно, для стационарного состояния уравнение непрерывности для вероятности примет вид:

.

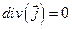Соответственно, вектор плотности вероятности для стационарного состояния имеет вид

.

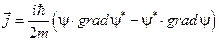Уравнение Шрёдингера для стационарного состояния.

Необходимым условием стационарности состояния является независимость от времени функции U, т.е. в стационарном состоянии эта функция однозначно трактуется как потенциальная энергия. В этом случае, подставим во временное уравнение Шрёдингера :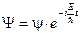

,

,

.

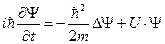Т.к. 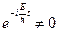, то можно сократить : 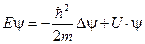. После преобразований получаем уравнение

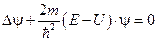
которое носит название уравнение Шрёдингера для стационарного состояния.

Дата добавления: 2014-01-07