Метод самосогласованного поля

Атом, как составную систему, можно полностью описать только полной волновой функцией. Однако такое описание практически невозможно для атомов сложнее атома водорода- самого простого из всех атомов химических элементов. Удобно применять приближённое описание- метод самосогласованного поля (метод Хартри-Фока). В этом методе вводится понятие о волновой функции каждого электрона. Волновая функция всей системы (атома) записывается как надлежащим образом симметризованое произведение одноэлектронных волновых функций. При вычислении волновой функции каждого электрона поле всех остальных электронов учитывается как внешний потенциал, зависящий в свою очередь от волновых функций этих остальных электронов.

В результате применения метода самосогласованного поля получается сложная система нелинейных интегро-дифференциальных уравнений. Нахождение явного решения такой системы является весьма трудоёмкой задачей.

Однако уравнения самосогласованного поля имеют вращательную симметрию (то есть они сферически симметричны). Это позволяет полностью классифицировать одноэлектронные волновые функции, из которых составляется полная волновая функция атома. Волновую функцию электрона в самосогласованном поле можно охарактеризовать квантовыми числами.

Квантовые числа.

Главное квантовое числоn может принимать любые целые положительные значения, начиная с единицы (n = 1,2,3, … ∞), и определяет общую энергию электрона на данной орбитали. Энергия для n = ∞ соответствует энергии одноэлектронной ионизации для данного энергетического уровня.

Орбитальное квантовое число l (называемое также азимутальным квантовым числом) определяет момент импульса электрона и может принимать целые значения от 0 до n - 1.

Орбитали принято называть по буквенному обозначению их орбитального числа:

Значение орбитального квантового числа l
Буквенное обозначение	s	p	d	f	g

Замечание. Буквенные обозначения атомных орбиталей произошли от описания спектральных линий в атомных спектрах: s (sharp) - резкая серия в атомных спектрах, p (principal)- главная, d (diffuse) - диффузная, f (fundamental) - фундаментальная.

Магнитное квантовое числоm определяет проекцию орбитального момента импульса на направление магнитного поля и может принимать целые значения в диапазоне от - l до l, включая 0 (m = - l … 0 … l).

Общее количество возможных состояний с одинаковым главным квантовым числом n с учётом двух возможных проекций спина на некоторое направление ­¯ равно .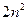

Геометрическое представление орбитали.

Для геометрического представления атомной орбитали указывают область пространства, в которой вероятность нахождения электрона не меньше определённого значения (обычно в диапазоне значений 0,9-0,99).

Поскольку энергия электрона определяется кулоновским взаимодействием и, следовательно, расстоянием от ядра, то главное квантовое число n задаёт размер орбитали.

Форма и симметрия орбитали задаются квантовыми числами l и m:

s - орбитали являются сферически симметричными,

p, d и f - орбитали имеют более сложную форму, определяемую угловыми частями волновой функции - угловыми функциями. Угловые функции Y_lm (φ, θ) - собственные функции оператора квадрата углового момента 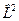, зависящие от квантовых чисел l и m, являются комплексными и описывают в угловых координатах (φ, θ) зависимость вероятности нахождения электрона в центральном поле атома. Линейная комбинация этих функций определяет положение орбиталей относительно декартовых осей координат.

Дата добавления: 2014-01-07