Лекция 2. Для выполнения предназначенных функций структура объекта должна быть упорядоченной – т.е

Для выполнения предназначенных функций структура объекта должна быть упорядоченной – т.е. она должна содержать элементы, соединенные между собой в определенной последовательности и передающие сигналы в заданном направлении. Однако в соответствии со 2-м законом термодинамики диссипативные процессы в замкнутых (изолированных) системах приводят к исчезновению любой упорядоченности, т.е. к хаосу. (происходит рост энтропии). Диссипативная система- система, рассеивающая энергию.

Если система открытая (обменивается с внешней средой энергией, веществом и информацией), то в ней возникают процессы самоорганизации: из хаоса рождаются некие упорядоченные устойчивые структуры. Обязательным условием самоорганизации системы является согласованное взаимодействие компонентов подсистем, которые составляют эту систему.

Это взаимодействие приводит к увеличению количества внутренних связей а не их распада при случайном изменении параметров. Во многих случаях современные автоматизированные системы представляют собой весьма сложные нелинейные открытые системы, способные к самоорганизации. Для таких сложных нелинейных систем невозможно построить аналитическую математическую модель.

Во-первых, неизвестно существуют ли решения такой модели, а если они есть, то какие и сколько. Во-вторых не поставлены математические задачи необходимости и достаточности. Нельзя даже записать с достаточной точностью систему уравнений.

Единственный на сегодняшний день эффективный вариант построения адаптивных моделей объектов (систем) с их последующей реализацией- это использование численных методов на типовых мультипроцессорных (распределенных) вычислительных системах. Такие системы можно считать активными. В них возможно управляемая самоорганизация (адаптация). Теоретической базой для построения подобных моделей и их реализации может являться Синергетика. От греч синергия = совместные действия.

Синергетика- один из современных подходов к исследованию сложных самоорганизующихся нелинейных управляемых систем. Синергетический подход базируется на представлении объекта и управляющей системы в виде распределенных подсистем. Эти подсистемы представляются из множества активных элементов. Активные элементы взаимодействуют между собой под действием управляющих сигналов. В результате этого взаимодействия изменяются состояния систем. Этим процессом можно управлять для получения требуемого состояния объекта \ системы. Управление по существ состоит в целенаправленном изменении свойств системы. Математическое описание явлений связанных с качественной перестройкой структуры системы, которая обменивается энергией и информацией с внешней средой, дает так называемая Теория катастроф.

Бифуркация — это приобретение нового качества в движениях динамической системы при малом изменении её параметров.

Простейший пример бифуркации системы может быть проиллюстрирован на переходе колебательной системы (звена) 2-го порядка в апериодическое звено 2 порядка или 2-х апериодических звеньев 1-го порядка при изменении параметров колебательной системы.

(1)

Или

(2)

(1)(2)- математическая модель исходной структуры

U(t)-управляющее воздействие \ исходный сигнал

y(t)-реакция системы

k- статический коэффициент передачи (параметр системы)

Tk= [секунды]- постоянная времени. Tk >0

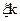- коэффициент демфирования

Оператор Лапласа: S=C0+ jw

P= d\dt = переменная дифференцирования.

Если 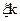удовлетворяет 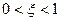(3),то исходная система является колебательной, устойчивой. Реакция такой системы на ступенчатое воздействие про нулевых начальных условиях (переходная характеристика) будет представлять собой затухающие колебания.

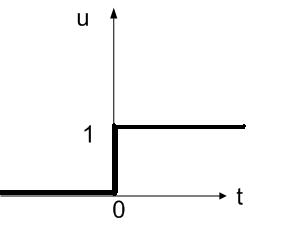
Корни характеристического уравнения математической модели (1)(2) в этом случае является комплексные, сопряженными с отрицательными вещественными частями.

(4)

,где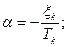

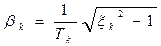
На комплексной плоскости: положение корней на при слови (3):

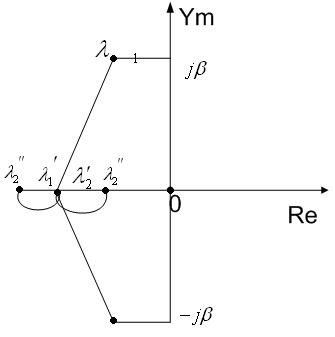
Если в результате каких-либо случайных или целенаправленных воздействий параметров 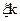начнет изменяться, например увеличиваться, то положение корней 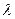будет меняться.

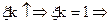
- корни вещественные, отрицательные, кратные.

Кратность корней- критический случай, т.е. неустойчивое равновесие -> физически это нереально.

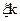=1 бифуркационное значение параметра 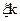. В критической точке реальная система находится не может, т.к. всегда существуют возмущения, выводящие систему из критической точки. Если возмущения будут приводить к увеличению 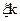, пока один из корней 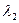не станет положительным, пройдя новую бифуркационную точку: система потеряет устойчивость.

В этом случае процесс в системе будет немонотонным затухающим (аппереодическим)

Вывод: апериодическая система 2-го порядка с корнями лямбда 1 с 2-мя штрихами и лямбда 2 с 2-мя штрихами может быть представлена качественно новой структурой, а именно последовательным соединением 2-х систем, каждая из которых 1-го порядка, соединенные последовательно.

Мат модели для новой структуры следующие:

Дата добавления: 2014-01-07