Общие положения об устойчивости сау

При изложении методики составления структурных схем и дифференциальных уравнений систем автоматического управления отмечалось, что первым вопросом исследования систем является вопрос об их устойчивости. Этот вопрос важен, во-первых, потому, что в большинстве случаев неустойчивые системы непригодны для практического использования, и, во-вторых, потому, что даже в устойчивой системе необходимо знать, какие запасы устойчивости она имеет.

В результате анализа устойчивости обычно недостаточно получить прямой и однозначный ответ на вопрос, устойчива ли система; в большинстве практически встречающихся случаев разработчику системы нужно ясно представлять, какие из параметров элементов системы наиболее сильно влияют на устойчивость и как следует их изменить, чтобы обеспечить необходимые запасы устойчивости.

Ранее было показано, что устойчивая система после окончания переходного процесса переходит в новое вынужденное состояние; устойчивость системы может быть определена в результате решения уравнений для свободного движения системы: однородного дифференциального или характеристического уравнений системы.

Решение однородного дифференциального уравнения системы имеет вид

(1)

где р_i — корни характеристического уравнения;

С_i — постоянные, определяемые из начальных условий.

Характеристическое уравнение n -гo порядка имеет n корней: p₁, p₂,…,.p_n. Эти корни могут быть действительными или комплексными попарно сопряженными.

Действительные корни дают в решении уравнения апериодическую составляющую вида

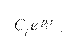
Очевидно, что если р_i<0, то это слагаемое с ростом t будет стремиться к нулю. Если же р_i≥0, то это слагаемое возрастает с ростом t и система будет неустойчивой. При р_i=0 это слагаемое становится равным C_i, т.е. общее решение системы, будет отличаться от частного решения на величину C_i.

Комплексные попарно сопряженные корни p_l=σ_l+jω_l и p_l=σ_l-jω_l соответствуют колебательным составляющим решения для свободного движения системы.

Если действительная часть комплексных сопряженных корней отрицательна (σ_l <0), то данная составляющая будет носить характер затухающих колебаний; если σ_l >0, то колебания будут нарастать, а при σ_l >0 они будут иметь постоянную амплитуду. Последние два случая (σ_l ≥0) приводят к неустойчивости системы.

Таким образом, система неустойчива, если хотя бы один из корней характеристического уравнения имеет положительную или равную нулю действительную часть. Следовательно, наиболее естественным методом определения устойчивости системы является решение ее характеристического уравнения и определение знаков действительных частей полученных корней. Однако такой метод хотя и позволяет получить ответ на вопрос об устойчивости системы, не может считаться приемлемым для большинства практических задач.

Это связано с математическими трудностями, возникающими при решении алгебраических уравнений высоких степеней. Поэтому на практике применяются другие методы, позволяющие, не прибегая к решению дифференциального или характеристического уравнения, а иногда даже и к составлению этих уравнений, получить все необходимые данные по устойчивости. Такие методы называются критериями устойчивости. Следует отметить, что все критерии устойчивости в той или иной форме используют тот факт, что у устойчивой системы действительные части всех корней характеристического уравнения отрицательны, однако знак действительных частей корней характеристического уравнения устанавливается не непосредственно в результате их определения, а косвенным путем.

Дата добавления: 2014-01-07