
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Способы выражения состава фаз
|
|
|
|
| Концентрация | Обозначение концентрации компонента А | ||
| в жидкой фазе | в газовой или паровой фазе | ||
| Мольная доля, кмоль А /кмоль (А+В) Массовая доля, кг А /кг (А+В) Относительная мольная концентрация (доля), кмоль А /кмоль В Относительная массовая концентрация (доля), кг А /кг В Объемная мольная концентрация, кмоль А /м3 (А+В) Объемная массовая концентрация, кг А /м3 (А+В) |
х
 Х
Х
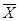 Сх
Сх

|
y
 У
У
 Су
Су

|
Для обратного пересчета выразим массовые доли х компонентов через мольные доли х.
Массы отдельных компонентов, содержащихся в 1 кмоль смеси, составляют МAхA,, МВхВ,,..., МКхК,..., МNхN, а общая масса 1 кмоль смеси составит

Соответственно массовая доля k -го компонента составит
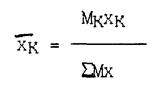 (1.2)
(1.2)
Знаменатель этой формулы, представляющий собой массу 1 кмоль смеси, называется средней молекулярной массой смеси.
Для двухкомпонентной (бинарной) смеси, состоящей из компонентов А и В, выражения (1.1) и (1.2) упрощаются.
Если массовая доля одного из компонентов (например, компонента А) равна хA, его мольная доля хA и молекулярный вес МA, то содержание другого компонента (с молекулярным весом МВ) будет (1 - хA) или (1 - хA) соответственно. Поэтому мольный состав смеси (по компоненту А) составит:
 (1.3)
(1.3)
а ее массовый состав по тому же компоненту составит
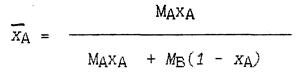 (1.4)
(1.4)
Пример 1: Определить мольный состав и среднюю молекулярную массу смеси бензола и толуола, содержащей 30 весовых процентов бензола.
Решение: Молекулярные массы компонентов: М1 = 78 (бензол) и М2 = 92 (толуол). По формуле (1.3) находим мольную долю бензола в смеси:
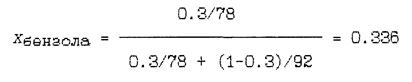
Мольная масса толуола Хтолуола = 1 - Хбензола = 0.664.
Средняя молекулярная масса смеси равна:

Сумма объемных массовых концентраций всех компонентов смеси равна массе 1 м3 смеси, т.е. плотности r:
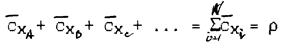
Таким образом, массовая доля k -го компонента смеси, выраженная через объемную массовую концентрацию этого компонента равна:
 (1.5)
(1.5)
Содержание компонентов газообразной смеси часто выражают через парциальные давления.
Под парциальным давлением компонента понимают давление, под которым бы находился данный компонент, если бы в отсутствии других компонентов он занимал весь объем смеси при ее температуре.
Согласно закону Дальтона, полное давление Р газовой смеси равно сумме парциальных давлений компонентов pА, рВ, pС, …:
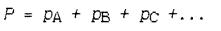
Как нетрудно убедиться, отношение парциального давления компонента к полному давлению равно объемной доле компонента в смеси. В самом деле, если парциальное давление k -го компонента р к, а объем газовой смеси V, то объем Vк, занимаемый этим компонентом при давлении Р, определяется из соотношения:
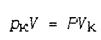
откуда
 (1.6)
(1.6)
а объемная доля компонента в смеси составит:
 (1.7)
(1.7)
Так как 1 кмоль любых компонентов занимает при одинаковой температуре один и тот же объем, то объемная доля Vк равна мольной доле ук компонента в газовой смеси. Таким образом:

| (1.8) |
Уравнение (1.8) устанавливает связь между парциальным давлением и мольной долей.
Теперь напишем уравнение состояния для 1 кг К -го компонента газовой смеси:
 (1.9)
(1.9)
где: р к - парциальное давление k -го компонент, Па;
R - газовая постоянная, равная 8314 Дж/(кмоль×град);
МК - молекулярная масса компонента.
Отсюда объем смеси, в которой будет находиться 1 кг компонента равен
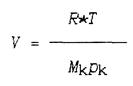 (1.10)
(1.10)
Согласно определению объемной массовой концентрации

или
 (1.11)
(1.11)
Уравнение (1.11) устанавливает связь между парциальным давлением и объемной массовой концентрацией.
При расчете состав газовой смеси, выраженный через парциальное давление компонента рк, часто приходится пересчитывать в относительный весовой состав. Это может быть сделано так.
Если общее давление Р, то парциальное давление носителя будет равно (Р - рк). Тогда уравнение состояния для компонента будет иметь вид:
 1.12)
1.12)
и для носителя
 (1.13)
(1.13)
где: V - объем смеси, м3;
Gk,Gн - количество компонента и носителя в объеме V, кг;
Мk, Мн - молекулярные массы компонента и носителя.
Деля уравнение (1.12) на уравнение (1.13), получим:
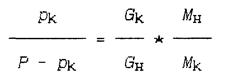
Отсюда находим относительный весовой состав:
 (1.14)
(1.14)
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 2675; Нарушение авторских прав?; Мы поможем в написании вашей работы!