Предельные производительность, спрос, предложения

ТЕМА 8: Исследование функций в экономике.

На основании экономического смысла производной и аппарата дифференциального исчисления возникает множество экономических задач, связанных с исследованием функций. В частности, представляют интерес экономические понятия и задачи на предельную производительность ресурса, предельный спрос продукции от цены и т.д.

Приведем определение и примеры таких задач.

Пример 1. Предприятие производит единиц некоторой однородной продукции в месяц. Исследовать финансовые накопления, если зависимость финансовых накоплений предприятия от объема выпуска выражается формулой

.

1. Из экономического смысла независимой переменной следует, что она неотрицательна. Итак,

.

2. . 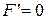при и . На промежутке производная положительна, на - отрицательна. В точке функция достигает максимума:

.

Вывод: финансовые накопления предприятия растут с увеличением объема производства до 100 единиц, при они достигают максимума, равного 39000 ден.ед., дальнейший рост производства приводит к сокращению финансовых накоплений.

Пример 2. Цементный завод производит тонн цемента в день. По договору он должен ежедневно поставлять строительной фирме не менее 20 т цемента. Производительные мощности завода таковы. Что выпуск цемента не может превышать 90 т в день. Определить, при каком объеме производства удельные затраты будут наибольшими (наименьшими), если функция затрат имеет вид:

.

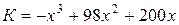Удельные затраты это средние затраты на единицу продукции, в данном случае на 1 т цемента. При объеме производства в т удельные затраты составят:

.

Задача сводится к отысканию наибольшего, наименьшего значения функции

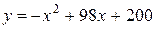
на промежутке .

Ответ:

Пример 3. Требуется оградить забором прямоугольный участок земли площадью 294 кв. м. и затем разделить его на две равные части перегородкой. Каковы должны быть размеры участка, чтобы на постройку забора и перегородки было истрачено наименьшее количество материала?

Указание. Обозначим ширину прямоугольного участка через х, а длину через у.

Из условий задачи следует, что х Î (0, + ¥).

Поскольку площадь участка равна 294 кв. м., то

х × у =S=294.

Откуда получаем, что

у =294/ х,

а общая длина Р всего загона равна:

Р(х) =3 х +2 у =3 х +2 ´ 294/ х

Таким образом, общая длина ограды представляет собой функцию от одной переменной х, и наша задача свелась к нахождению наименьшего значения этой функции в интервале (0, + ¥).

Ответ: .

Дата добавления: 2014-01-07