Лекция 6

Алгоритмы силового расчета групп Ассура 2-го класса

Силовой расчет групп Ассура 2-го класса

. Силовой расчет групп Ассура 2-го класса 1-го вида

Сначала определяются все активные силы (силы тяжести звеньев, силы технологического сопротивления), а также силы и моменты сил инерции звеньев. Векторы этих сил прикладываются на план группы Ассура, вычерченный в масштабе.

Изобразим в масштабе группу Ассура 2-го класса 1-го вида (рис. 4.3) и приложим к звеньям группы все силы и моменты пар сил. При этом все силы, действующие на звено, приведем к одной силе, все моменты пар сил – к одному моменту.

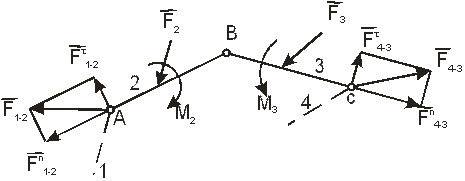
Рис. 4.3. Группы Ассура 2-го класса 1-го вида с приложенными к ним силами и моментами пар сил

Примем следующие обозначения. Звено, к которому присоединяется звено AB обозначим номером 1, звено AB – номером 2, звено BС – номером 3, звено, присоединенное к BС, – номером 4. Силы и моменты пар сил имеют индексы номеров звеньев, к которым они приложены.

Силы взаимодействия звеньев будем обозначать двумя цифрами, разделенными чертой. Первая цифра обозначает номер звена, которое действует на звено, обозначенное второй цифрой, например: F _1-2 – сила действия звена 1 на звено 2.

Пусть звенья группы Ассура 2-го класса 1-го вида нагружены силами F ₂ и F ₃ и моментами M ₂ и M ₃. Требуется определить реакции в кинематических па

рах A, B и C, т.е. F _1-2, F _2-3, F _4-3, которые являются силами взаимодействия звеньев.

У реакций F _1-2 и F _4-3 известны только точки их приложения – в центре шарниров A и C. Для определения величин этих сил раскладываем каждую из них на две составляющие. Реакцию F _1-2 разложим на F _1-2 ⁿ – нормальную, направленную вдоль звена АВ, и F _1-2^τ – касательную, направленную перпендикулярно звену АВ. Составляющие реакции F _4-3 разложим на F _4-3 ⁿ – нормальную, направленную вдоль звена ВС, и F _4-3^τ – касательную, направленную перпендикулярно звену ВС.

Определим составляющие 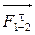и 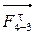из уравнения равновесия звеньев 2 и 3, рассмотренных по отдельности.

Из условия равновесия моментов сил, действующих на звено 2 относительно точки В, имеем

∑ M_{B (звена 2)} = – M ₂ + M_B (F ₂) – F ^τ _1-2 l_AB = 0,

откуда

F ^τ _1-2 = [– M ₂ + M_B (F ₂)] / l_AB,

где M_B (F ₂) – момент силы F ₂ относительно точки B; l_AB – длина звена AB.

Если после определения F _1-2^τ она окажется отрицательной, то ее истинное направление должно быть выбрано противоположным.

Аналогичным образом определяем величину составляющей F _4-3^τ, рассматривая равновесие звена BС:

∑ M_{B (звена 3)} = M ₃ – M_B (F ₃) + F ^τ _4-3 l_CB = 0;

F ^τ _4-3 = [– M ₂ + M_B (F ₃)] / l_CB.

Здесь M_B (F ₃) – момент силы F ₃ относительно точки B.

Теперь рассмотрим равновесие всех сил, действующих на группу Ассура. Уравнение равновесия сил запишем в векторной форме, начиная с известных сил. Неизвестные нормальные составляющие реакций записываем в конце уравнения:

.

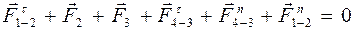Последнее уравнение равновесия решаем графически путем построения плана сил (рис. 4.4). Силовой многоугольник должен быть замкнутым. Строим силовой многоугольник в соответствии с последним уравнением. Из произвольной точки k отложим вектор ^τ _1-2 , затем последовательно суммируем силы ₂, ₃, ^τ _4-3. Все векторы строим с масштабным коэффициентом μ _F.

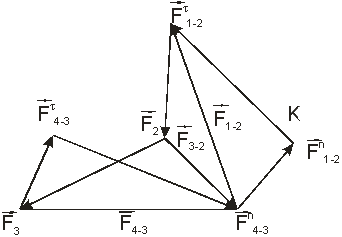
Рис. 4.4. План сил группы Ассура 2-го класса 1-го вида

Замкнем силовой многоугольник следующим образом. Из конца вектора ^τ _4-3 проведем прямую по направлению ⁿ _4-3 , а из точки k – прямую по направлению ⁿ _1-2. В точке пересечения этих прямых будут находиться конец вектора ⁿ _4-3 и начало вектора ⁿ _1-2. Векторы 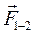и 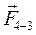получаем в соответствии с уравнениями

; .

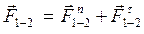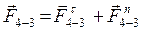Для определения реакции в кинематической паре B рассмотрим равновесие 2 -го звена, мысленно отсоединив звено 3. Действие звена 3 заменим силой F _3-2. Запишем условие равновесия сил, действующих на звено AB:

_1-2 + ₂ + _3-2 = 0.

Строим это уравнение, используя уже построенный план сил. Для определения _3-2 необходимо замкнуть силовой треугольник в соответствии с последним уравнением, т.е. соединить конец вектора ₂ с началом вектора _1-2 .

Силовой расчет группы Ассура 2-го класса 2-го вида

Группа второго вида имеет одну внешнюю поступательную пару C с направляющей x-x (рис. 4.5). На звенья группы действуют известные силы F ₂ и F ₃, а также пары сил с моментами M ₂ и M ₃. Длины звеньев и точки приложения сил также заданы.

Требуется определить _1-2, _3-2, _0-3 и плечо силы _0-3 относительно точки B.

Для реакции _1-2 известна точка ее приложения, неизвестными являются направление и величина. Реакция 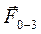перпендикулярна к оси x-x направляющей. Неизвестными являются точка ее приложения и величина.

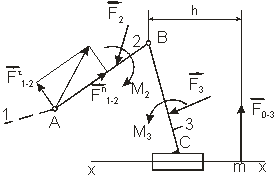
Рис. 4.5. Группа Ассура 2-го класса 2-го вида

Разложим силу _1-2 на две составляющие – нормальную 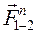, направленную вдоль звена АВ, и касательную ^τ_1-2, направленную по нормали к прямой АВ.

Величину составляющей F ^τ _1-2 определим из условия равновесия моментов сил, действующих на звено 2 относительно точки В:

∑ M_{B (звена 2)} = – M ₂ + M_B (F ₂) – F ^τ _1-2 l_AB = 0.

Откуда F ^τ _1-2 = [– M ₂ + M_B (F ₂)] / l_AB,

где M_B (F ₂) – момент силы F ₂ относительно точки B.

Рассмотрим равновесие сил, действующих на группу Ассура:

.

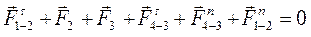В этом уравнении неизвестны по величине силы 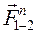и _0-3. Построим план сил, для чего из произвольной точки k (рис. 4.6) откладываем в выбранном масштабе сил μ_F вектор _1-2 , к нему последовательно прибавляем силы ₂ и ₃ в том же масштабе. Замыкая силовой многоугольник, находим ⁿ _1-2 и _0-3.

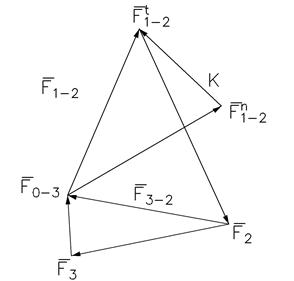
Рис. 4.6. План сил группы Ассура 2-го класса 2-го вида; μ_F =..., Н/мм.

Реакцию в паре B определим из условия равновесия сил звена AB, которые запишем в векторной форме:

.

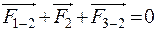Таким образом, для определения _3-2 достаточно соединить на имеющемся плане сил конец вектора ₂ с началом вектора_1-2.

Плечо h силы_0-3 относительно точки B определим из следующего условия равновесия моментов, действующих на звено BC относительно точки B (рис. 6.4):

∑ M_{B (звена 3)} = M ₃ – M_B (F ₃) + F _0-3 h = 0, откуда h = [ M_B (F ₃) – M ₃] / F _0-3 .

Здесь M_B (F ₃) – момент силы F ₃ относительно точки B.

Силовой расчет группы Ассура 2-го класса 3-го вида

Группа Ассура 2-го класса 3-го вида, изображенная в масштабе μ _l, показана на рис. 4.7, а. Заданы силы ₂ и ₃, а также пары сил с моментами M ₂ и M ₃, действующие на звенья. Штриховыми линиями обозначены звенья 1 и 4, к которым была присоединена группа Ассура. Действие этих звеньев заменяем реактивными силами _1-2 и _4-3 .

Требуется определить _1-2, _-3 , _4-3 и плечо h силы _2-3 относительно точки B.

Разложим реакцию _4-3 на ортогональные составляющие ^τ_4-3 и ⁿ _4-3. Силу ⁿ _4-3 направим по линии АС, соединяющей вращательные пары, а ^τ_4-3 − перпендикулярно линии АС.

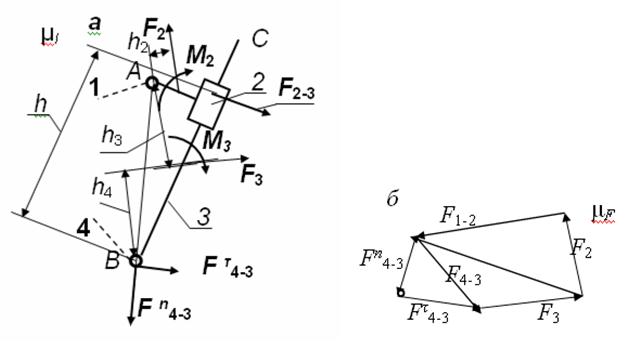РРис. 4.7. Силовой расчет групп Ассура 2-го класса 3-го вида:

а − план группы Ассура, выполненный в масштабе μ _l, м/мм; б − план сил, выполненный в масштабе μ _F, Н/мм.

В зоне поступательной кинематической пары приложим реакцию _2-3 перпендикулярно линии ВС. Величину составляющей F ^τ_4-3 определим из

условия равновесия моментов сил, действующих на группу Ассура относительно точки А звена AB:

Σ М_{А (гр. Ассура)}= − М ₂ − М ₃ + F ₂ h ₂ μ _l + F ₃ h ₃ μ _l + F ^τ_4-3 l_АВ = 0.

Откуда

F ^τ_4-3 = (М ₂ + М ₃ − F ₂ h ₂ μ _l − F ₃ h ₃ μ _l) / l_АВ.

Из условия равновесия векторов сил, действующих на звено 3, имеем

Σ _{(Звена 3)}= ^τ_4-3 + ₃ + _2-3 + ⁿ _4-3 = 0.

По этому уравнению построим план сил для звена 3, начиная с точки, отмеченной кружком (рис. 4.7, б). Из плана сил находим _2-3 и ⁿ _4-3.

Запишем условия равновесия векторов сил, действующих на звено 2

Σ _{(Звена 2)}= _3-2 + ₂ + _1-2 = 0

и дополним существующий план сил графическим решением этого уравнения. Умножая длины векторов реактивных сил, изображенных на плане сил, получим абсолютные значения неизвестных реакций.

Плечо h приложения силы _2-3 найдем из следующего уравнения:

Σ М_{В (звена 3)}= − М ₃ − F ₃ h ₄ μ _l − F _2-3 h = 0.

Откуда

h = (− М ₃ − F ₃ h ₄ μ _l) / F _2-3.

В плане сил (рис. 4.7, б) вектор _2-3 направлен противоположно этому же вектору в расчетной схеме (рис. 4.7, а). Поэтому в последнем равенстве величину силы F _2-3 следует ставить со знаком минус.

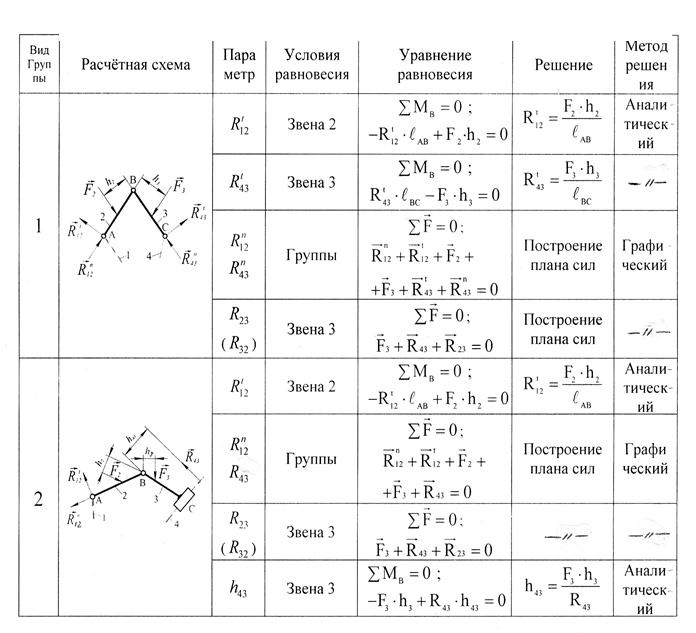
Алгоритмы силового расчета группы Ассура 2-го класса различных видов представлены в нижеследующей табл. 4.1.

Таблица 4.1

Алгоритмы силового расчета групп Ассура 2-го класса.

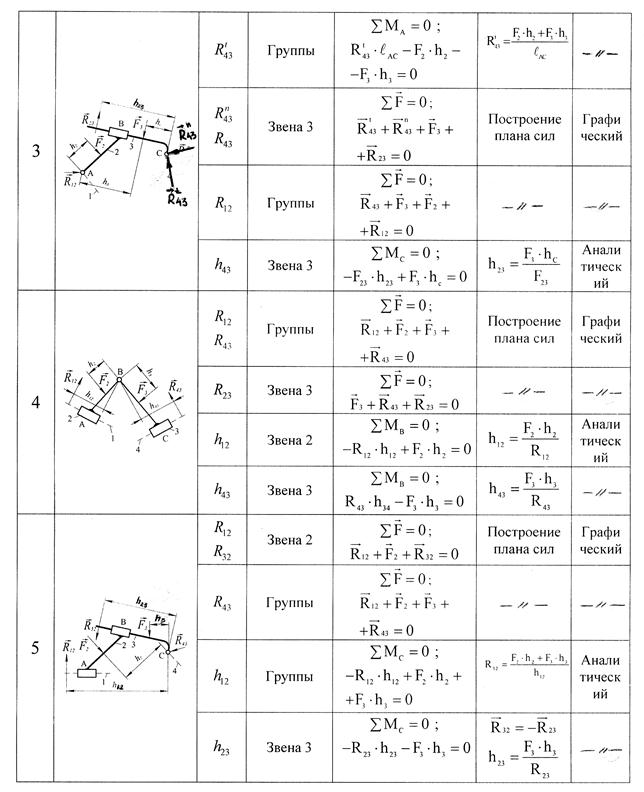Сначала определяются все активные силы (силы тяжести звеньев, силы технологического сопротивления), а также силы и моменты сил инерции звеньев. Векторы этих сил прикладываются на план группы Ассура вычерченный в масштабе. В табл. 4.1 эти силы заменены их равнодействующими F₁ и F₂.

Затем прикладываются составляющие неизвестных реакций R₁₂, R₄₃, R₂₃ в кинематических парах. Далее определяются неизвестные величины и направления реакций.

Дата добавления: 2014-01-07