Свойства и элементы эвольвентного зацепления

Рассмотрим внешнее эвольвентное зацепление цилиндрических колёс, когда начальные окружности касаются внешним образом (рис. 5.5).

Радиусами r_{a 1} и r_{a 2} и r_{f 1} и r_{f 2} проведём окружности вершин и впадин, ограничивающие соответственно головки и ножки зубьев. Переход эвольвентного профиля зуба в окружность впадин должен быть плавным по окружности со стандартным радиусом r = 0,25 m. Затем откладываем по начальной окружности толщину зуба первого колеса и толщину зуба второго колеса равную ширине впадины первого колеса. Строим обычным путём симметричные профили. Точки пересечения окружностей выступов и линии NN обозначим через a и b.

Докажем первое свойство эвольвентного зацепления, что два эвольвентных профиля обеспечивают постоянство передаточного отношения.

В соответствии с основной теореме зацепления для постоянного передаточного отношения u ₁₂ = ω₁ /ω₂ = const общая нормаль к профилям зубьев должна проходить через неподвижную точку Р на линии центров.

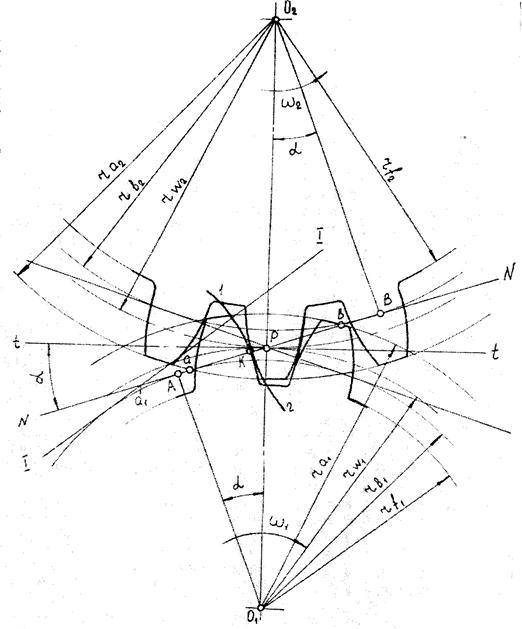
Рис. 5.5. Внешнее эвольвентное зацепление

Нормаль, проведенная к эвольвентному профилю зуба колеса 1, из третьего свойства эвольвенты касается основной окружности с радиусом r_{b 1}. Нормаль, проведенная к эвольвентному профилю зуба колеса 2, по тем же соображениям касается основной окружности колеса 2. В точке контакта K должна существовать общая нормаль NN. Следовательно линия NN – касается обеих основных окружностей, на которых образованы эвольвенты, проходит через неподвижную точку Р на межосевой линии.

Следовательно, эвольвенты удовлетворяют основной теореме зацепления и обеспечивают постоянство передаточного отношения.

Точка K контакта зубьев располагается на линии NN, связанной с неподвижной плоскостью. Так как точка K была принята произвольной, то линия NN представляет собой геометрическое место точек контакта зубьев на неподвижной плоскости называется линией зацепления. Вне этой линии зубья не контактируют.

Рассмотрим процесс зацепления пары зубьев и установим границы линии зацепления. Если расположить зуб первого колеса так, что его профиль будет проходить через точку а, то у контактирующего с ним зуба второго колеса эвольвента в точке а будет располагаться своей верхней точкой, которая первой попадает на линию NN. Следовательно, на линии NN точка а будет началом зацепления. Дальнейшее перемещение точки контакта зубьев по линии зацепления будет происходить до точки b, после которой зацепление уже невозможно, так как эвольвента зуба первого колеса уходит с линии зацепления. Таким образом, зацепление пары зубьев будет происходить в пределах линии 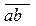, которая называется активной линией зацепления.

Линия АВ называется линией зацепления. Это есть предел активной линии зацепления. Рабочие участки зубьев – это участки их профилей, точки которых в процессе зацепления контактируют, передавая движение.

Согласно формуле (5.4)

u ₁₂ = ω₁ /ω₂ = (O ₂ B)/(O ₁ A) = r_{b 1} / r_{b 2} = const.

Полученное выражение указывает на второе свойство эвольвентного зацепления, что изменение межосевого расстояния a_w. не влияет не передаточное отношение. Это позволяет назначать более широкие допуски на изготовление и монтаж колес.

Изменяя параметры зубчатого зацепления (например, радиусы r_{a 1} и r_{a 2}), можно удлинить линию 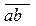, при этом точки а и b не могут располагаться соответственно за точками А и В. Действительно, если предположить, что точка а заняла положение а₁ (см. рис. 5.5), то нормаль к эвольвенте будет касательной I-I к основной окружности и уже не пройдёт через точку Р, т.е. за пределами линии АВ не удовлетворяется основной закон зацепления. В этом случае эвольвенты пересекутся. Это явление называется интерференцией зубьев. В зацеплении колес интерференция ведет к заеданию и заклиниванию передачи.

Рис. 5.6. Подрезание зуба колеса.

При изготовлении колес интерференция ведет к подрезанию зубьев, что выражается в срезании режущими кромками инструмента части эвольвентного профиля выше основной окружности и в ослаблении зуба (рис. 5.6).

Реечное зацепление (рис. 5.7) предназначено для преобразования вращательного движения зубчатого колеса в поступательное движение зубчатой рейки (возможно и обратное). Профиль зуба рейки прямолинеен.

Рис. 5.7. Реечное зубчатое зацепление

Дата добавления: 2014-01-07