Приведение сил и масс в механизмах

При составлении динамических моделей механических систем удобно массы и моменты инерции различных звеньев, соединенных кинематическими связями, заменить одной приведенной массой (моментом инерции). К этой массе прикладываются приведенные силы, эквивалентные силам, действующим на приводимые звенья. Если рассматривается жесткая модель механизма с одной степенью подвижности, то для его изучения достаточно знать закон движения одного из звеньев, как правило, начального. Динамическая модель такого механизма показана на рис. 8.1. Звено механизма, к которому приведены массы (моменты инерции) на динамические модели, называется звеном приведения сил и масс. Точки сосредоточения приведенных масс – точки приведения.

Приведенной массой называется такая условная масса, сосредоточенная в точке приведения, кинетическая энергия Т _пр которой равна сумме кинетических энергий приводимых звеньев (рис. 8.1.б).

Кинетическая энергия Т_i i -го звена и приведенной массы Т _пр соответственно равны

; .

Согласно определению приведенная масса

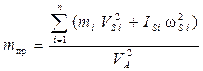. (8.2)

Если массы звеньев приводятся к эвену, вращающемуся вокруг неподвижной оси, то удобнее пользоваться понятием приведенного момента инерции I_np этих масс относительно оси вращения звена приведения

, (8.2, а)

где m_i, I_{S i} – масса и осевой момент инерции относительно оси, проходящей через центр масс i -го звена; V_{S i}, ω_i – соответственно скорость масс i -го звена и угловая скорость i -го звена; V_A – скорость точки приведения; ω _ОА – угловая скорость звена приведения.

Приведенной силой (моментом) называют условную силу (момент), которая, будучи приложена к звену приведения, развивает мощность N, равную мощности приводимых сил и моментов.

Величина приведенной силы, направленной по скорости точки приведения, равна

(8.3)

Приведенный момент силы равен

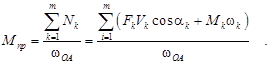
(8.3,а)

где F_к – величина приводимой силы, приложенной в точке к механизма;

V _к – скорость точки k; α _к – угол между векторами 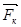,; М_к – момент, приложенный к звену k; ω _k – угловая скорость k -го звена.

Из формул (8.2), (8.3) следует, что приведенная масса и приведенная сила зависят от отношения квадратов скоростей приводимых звеньев к квадрату скорости звена приведения. Известно, что отношение скоростей определяется только соотношением длин звеньев механизма и обобщенной координатой равной угловой координате φ звена приведения ОА. Таким образом, приведенная сила и приведенная масса являются функцией обобщенной координаты φ.

Пример: На рисунке представлен синусный механизм. При движении ползуна вправо на него действует постоянная сила сопротивления F_с, направленная влево. Построить графики F _пр.с и m _пр, учитывая только массу ползуна.

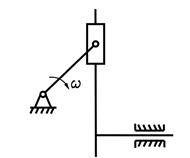
Синусный механизм

Дата добавления: 2014-01-07