Уравнения движения

Для определения закона движения звеньев приведения по заданным силам используются уравнения движения. Уравнения движения могут быть представлены в различных формах. Для механизмов с жесткими звеньями с одной степенью свободы, когда моменты движущих сил сопротивления зависят только от обобщенной координаты q, удобнее пользоваться уравнениями движения в форме уравнения изменения кинетической энергии (8.1):

Т – Т ₀ = Σ А.

С учетом введенных понятий о приведенных силах и массах уравнения движения примут вид:

а) уравнение движения в формеразности кинетических энергий (8.1)

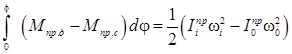, (8.1, а)

где М_пр.д и М_пр.с приведенный момент движущих сил и сил сопротивления соответственно; , - приведенные моменты инерции соответственно в i -том и нулевом положениях механизма; ω _i, ω₀ – угловые скорости звена приведения в началь­ном и рассматриваемом положениях механизма; φ – обобщенная координата, т.е., как правило, угол поворота звена приведения.

Для механизмов с одной степенью свободы, когда моменты сил зависят от обобщенной координаты φ и ее производной ω, используют уравнение Лагранжа второго рода

, (8.4)

где Т – кинетическая энергия; Q – обобщенная сила; t – время.

Обобщенная сила Q определяется из условия равенства элементарных работ этих сил на возможных перемещениях точек приложении этих сил работам внешних сил, действующих на механизм на возможных перемещениях точек их приложения. Для механизмов с одной степенью подвижности обобщенная сила

,

где F_пр.д и F_пр.с – приведенные силы движущая и сопротивления соответственно

После преобразований выражения (8.4) получим:

(8.5)

С учетом введенных понятий о приведенных силах и массах уравнения движения примут вид:

а) уравнение движения в интегральной форме

, (8.1, а)

где 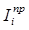, 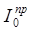– приведенные моменты инерции соответственно в i -ом и нулевом положениях механизма; ω ₀ и ω _i – угловые скорости звена приведения в начальном и рассматриваемом положениях механизма; φ – угол поворота звена приведения.

б) уравнение движения в дифференциальной форме:

. (8.5, a)

Дата добавления: 2014-01-07