Основные формулы комбинаторики

Комбинаторика – раздел математики, изучающий вопросы о том, сколько комбинаций определённого типа можно составить из данных предметов (элементов).

Правило суммы: пусть имеется n попарно непересекающихся множеств A ₁, A ₂, …, A_n, содержащих m ₁, m ₂, …, m_n элементов соответственно. Число способов, которыми можно выбрать один элемент из всех этих множеств, равно

m ₁ + m ₂ + … + m_n.

Кортеж – конечная последовательность (допускающая повторения) элементов какого-нибудь множества.

Правило произведения: пусть имеется n множеств A ₁, A ₂, …, A_n содержащих m ₁, m ₂, …, m_n элементов соответственно. Число способов, которыми можно выбрать по одному элементу из каждого множества, т. е. построить кортеж (а ₁, а ₂,..., а_n), где а_i Î А_i (i = 1, 2, …, n), равно

m ₁ ּ m ₂ ּ … ּ m_n.

Определение 1. Размещениями из n различных элементов по m элементов (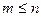) называют комбинации, составленные из данных n элементов по m элементов, которые отличаются либо самими элементами, либо порядком элементов.

Пример. Из трёх элементов a, b, c можно составить следующие размещения по два элемента: ab, ac, bc, ba, ca, cb.

Число различных размещений без повторений из n элементов по m элементов определяется по формуле:

.

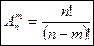Размещения с повторениями (n различных элементов, элементы могут повторяться):

.

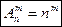Пример. Возьмем буквы Б, А, Р. Какие размещения из этих букв, взятых по две, можно получить? Сколько таких наборов получиться, если: 1) буквы в наборе не повторяются; 2) буквы могут повторяться?

1) Получатся следующие наборы: БА, БР, АР, АБ, РБ, РА.

.

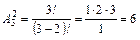2) Получатся наборы: ББ, БА, БР, АА, АБ, АР, РР, РБ, РА.

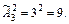
Определение 2. Перестановками из n различных элементов называют размещения из этих n элементов по n.

Перестановки можно считать частным случаем размещений при m=n. Тогда число всех перестановок без повторений из n элементов вычисляется по формуле:

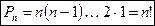
Перестановки с повторениями (k различных элементов, где элементы могут повторяться 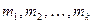раз и 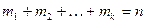, где n – общее количество элементов):

.

Пример. Возьмем буквы Б, А, Р. Какие перестановки из этих букв можно получить? Сколько таких наборов получится, если: 1) буквы в наборе не повторяются; 2) буква А повторяется два раза?

1) Получатся наборы: БАР, БРА, АРБ, АБР, РАБ, РБА.

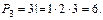
2) Получатся наборы: БАРА, БРАА, БААР, ААРБ, ААБР, АБАР, АРАБ, АРБА, АБРА, РАБА, РААБ, РБАА.

Определение 3. Сочетаниями из n различных элементов по m элементов называются комбинации, составленные из данных n элементов по m элементов, которые отличаются хотя бы одним элементом.

Отметим разницу между сочетаниями и размещениями: в первых не учитывается порядок элементов.

Число сочетаний без повторений из n различных элементов по m элементов вычисляется по формуле:

.

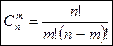Пример. В лабораторной клетке содержат трёх белых и трёх коричневых мышей. Найдите число способов выбора двух мышей, если они могут быть любого цвета.

m=2, n =6, тогда.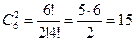

Сочетания с повторениями (n элементов, взятых по m, где элементы могут повторяться):

.

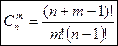Пример. Возьмем плоды: банан (Б), ананас (А) и репа(Р).Какие сочетания из этих плодов, взятых по два, можно получить? Сколько таких наборов получится, если: 1) плоды в наборе не повторяются; 2) можно брать по два одинаковых плода?

1) Получатся наборы: БА («банан, ананас» и «ананас, банан» – один и тот же набор), АР и РБ.

.

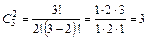2) Получатся наборы: ББ, БА, БР, АА, АР, РР.

.

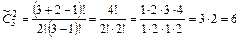Дата добавления: 2014-01-07