Оценка точности равноточных измерений

Классификация измерений и ошибок измерений

Элементы теории ошибок измерений

а) Понятие измерений. Виды измерений

При геодезическом обеспечении строительства выполняется большой объём геодезических измерений.

Под измерениями понимают процесс сравнения некоторой физической величины с величиной того же рода, принятой за единицу измерения (например, длина линии на местности, закреплённая колышками, сравнивается с мерным прибором - землемерной лентой, рулеткой и т.д.).

Измерения подразделяются на прямые и косвенные.

Прямыми измерениями называют непосредственное сравнение единицы меры (например, рулетки, землемерной ленты) с объектом.

Случаи, когда измеряют одни величины, а определяемое значение вычисляют как функцию результатов измерений называют косвенными измерениями. Например, при определении площади какого-либо объекта прямоугольной формы нецелесообразно выполнять прямые измерения, взяв за единицу меры квадрат со стороной 1 м и укладывая его на определяемой площади. Целесообразно измерить длину и ширину объекта и вычислить площадь как произведение этих величин.

б) Классификация ошибок измерений

Известно, что всякие измерения сопровождаются ошибками, обусловленными рядом факторов (условиями измерений, опытом наблюдателя, точностью прибора и т.д.).

Под ошибкой измерения понимают разность между результатом измерений l и истинным значением измеряемой величины Х

= l - X. (1)

По характеру влияния на результаты измерений различают следующие виды ошибок:

- грубые ошибки - это, как правило, просчёты. Например, при измерении линии длиной 15 м 50 см взяли отсчёт 16 м 50 см, т.е. грубо ошиблись на 1 м. Чтобы обнаружить грубую ошибку (промах), необходимо измерения повторить, по возможности другими методами;

- систематические ошибки - это, как правило, ошибки, входящие в результаты измерений по определённой математической зависимости. Это постоянная составляющая общей ошибки измерений или закономерно изменяющаяся ошибка при повторных измерениях одной и той же величины.

Например, длину линии измеряют рулеткой, номинальная длина которой 10 м (l _н = 10 м). Рулетка уложилась в измеряемой линии 5 раз (n = 5). Результат измерения линии равен D _н = l _н х n = 10 х 5 = 50 м.

Допустим, что в момент измерений длина рулетки была не 10 м, а 9.90 м, т.е. фактическая длина рулетки l_ф = 9.90 м. Тогда длина линии Д _ф = l _ф* 5 = 9.90 _* 5 = 49. 50 м, а систематическая ошибка = Д _н - Д _ф = = 50.00 - 49.50 = + 0.50 м.

Если разность длин мерного прибора обозначить через l = l _н - l _ф, то систематическую ошибку можно вычислить по формуле

= n _* l. (2)

Для ослабления систематических ошибок применяют следующие способы:

- в результаты измерений вводят поправки, равные по величине, но с противоположным знаком;

- выбирают методику измерений, при которой ошибки входят в результаты измерений с противоположными знаками;

-выполняют измерения в условиях, при которых систематическая ошибка по абсолютной величине не превысит определённого малого значения.

- случайные ошибки - ошибки величину и знак которых точно предсказать невозможно. Случайная ошибка неизбежна и порождается условиями измерений.

в) Свойства случайных ошибок

1 Свойство компенсации: сумма случайных ошибок, делённая на их число при неограниченном увеличении количества измерений n стремится у нулю

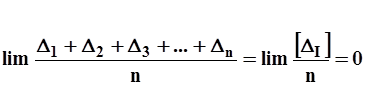. (3)

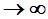n n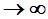

2. Свойство симметричности относительно нуля: положительные и отрицательные ошибки, равные по абсолютной величине, появляются с одинаковой вероятностью.

3. Свойство рассеивания: сумма квадратов случайных ошибок, делённая на их число n, при неограниченном числе измерений стремится к своему стандарту m²₀, называемому теоретическим значением средней квадратической ошибки, т.е.

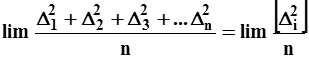= m²₀. (4)

n®¥ n®¥

4 Свойство ограниченности: случайная ошибка по абсолютной величине не превышает некоторого предела _пр, называемого предельной ошибкой

_i £ _пр. (5)

5 Свойство плотности: чем больше по абсолютной величине случайная ошибка, тем реже она встречается и, наоборот, чем меньше случайная ошибка тем чаще она появляется.

Измерения, выполненные в одинаковых условиях, равным числом приёмов измерений, одним и тем же прибором называют равноточными.

а) Понятие точности измерений, арифметической средины

Дата добавления: 2014-01-07