
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Определение предела функции в точке
|
|
|
|
Определение 1. Последовательность {x} называется последовательностью Гейне (для точки а и множества {x}), если
xn Î{x}, {x}®a, xn¹a.
Определение 2. (определение предела по Гейне) Число b называется пределом функции y=f(x) в точке а 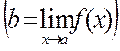 , если для любой последовательности Гейне {xn}соответствующая последовательность значений функций {f(xn)}сходится к числу b.
, если для любой последовательности Гейне {xn}соответствующая последовательность значений функций {f(xn)}сходится к числу b.
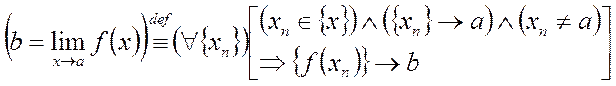
Таким образом, для доказательства того, что функция y=f(x) не имеет предела в т. а (в смысле определения по Гейне), достаточно указать две последовательности Гейне {x1n}и {x11n}, для которых
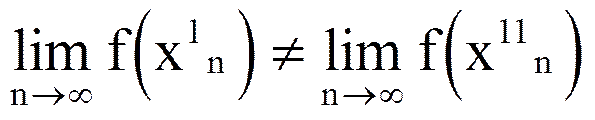
Пример 1. Функция Дирихле y=D(x) не имеет предела в т. a=0.
Действительно,
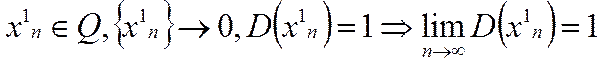
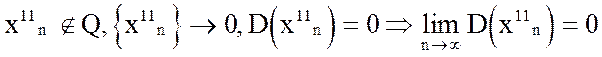 .
.
Пример 2. Функция y=sgnx не имеет предела в т. а=0.
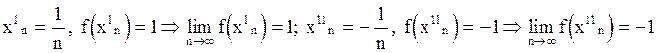
Определение 2. * (определение предела по Коши). Число b называется пределом функции y=f(x) в точке а, или при x®a ( ), если для любого положительного числа e найдется положительное число d такое, что для всех значений аргумента x, удовлетворяющих условию
), если для любого положительного числа e найдется положительное число d такое, что для всех значений аргумента x, удовлетворяющих условию
0<½x-a½<d, будет выполняться неравенство ½f(x)-b½<e.
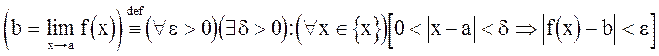 .
.
Замечание 1. Условия xn ¹a и 0<½x-a½ в определениях 2 и 2* исключают из рассмотрения т. а. В этой точке функция y=f(x) может быть не определена, либо ее значение может быть отличным от b. Таким образом, предел функции в т. а не зависит от значения функции в этой точке.
Замечание 2. Условие
0<½x-a½<d Û(a-d < x < a+d)Ù(x¹a) Û
x принадлежит проколотой d - окрестности т. а. Условие ½f(x)-b½<e Û
b-e< f(x)<b+e Û f(x) принадлежит e - окрестности т. b. Это условие означает, что точки графика функции y=f(x) с координатами (x, f(x)) попадают в e полоску
{b-e<y<b+e} прямой y=b.

Рис. 4
Замечание 3. В определении 2* достаточно найти d= d(e) только для малых e>0. Так как из неравенства e1 < e2 и ½f(x)-b½<e1 , очевидно, следует неравенство ½f(x)-b½<e2 для тех же значений x (и, следовательно, для d(e2)= d(e1)).
С другой стороны, если d(e) найдено лишь для достаточно больших e, то этого может быть недостаточно для существования предела функции (см. рис.5)
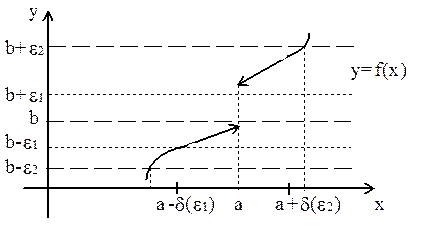
Рис. 5
Очевидно, для e1>0 нельзя найти d(e1), для которого при всех x из проколотой d(e1) - окрестности т. а график попадал бы в e1 - полоску y=b. (Для e2>0 такое d(e2) существует).
Замечание 4. Если в определении 2* по данному e> 0 найдено d= d(e)>0,
то любое d1: 0<d1 <d(e) такое можно взять в качестве d. Действительно,
0<½x-a½<d1 Þ 0<½x-a½<d(e) Þ½f(x)-b½<e. Отсюда следует, что в определении 2* не нужно искать наибольшее возможное значение d по данному значению e> 0.
Замечание 5. Определение 2* можно сформулировать следующим образом: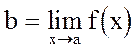 , если для любой e - окрестности точки b, существует такая d- окрестность т. а, что для всех значений аргумента x, принадлежащих этой d- окрестности и отличных от а, значение функции f(x) попадает в e - окрестность т. b.
, если для любой e - окрестности точки b, существует такая d- окрестность т. а, что для всех значений аргумента x, принадлежащих этой d- окрестности и отличных от а, значение функции f(x) попадает в e - окрестность т. b.
Замечание 6. В определении предела требуется существование симметричной окрестности (d- окрестности) точки а, но для e - окрестности т. b, может существовать несимметричная большая окрестность. (см. рис. 2).
Теорема. Определения 2 и 2*предела функции по Гейне и Коши эквивалентны.
Пример 3. Доказать по определению, что 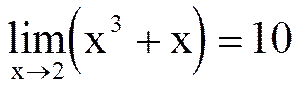 .
.
Запишем определение предела по Коши для данной функции.
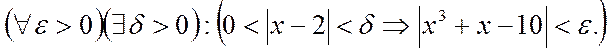
Задача состоит в том, чтобы по e найти d, при котором справедлива эта импликация.
Рассмотрим неравенство ½x3 +x-10½< e и будем искать часть множества его решений вида
½x-2½< h(e), тогда h(e) можно будет взять в качестве d.
x3 + x-10= x3 - 8+ x-2=
(x-2)(x2 +2x+4+1)
½x3 + x-10½< 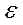 Û½x-2½½x2 +2x +5½<e.
Û½x-2½½x2 +2x +5½<e.
Рассмотрим сегмент [1, 3], на котором функция x2+2x+5 является ограни четной: ½x2 +2x+5½£ 9+6+5=20, тогда
четной: ½x2 +2x+5½£ 9+6+5=20, тогда
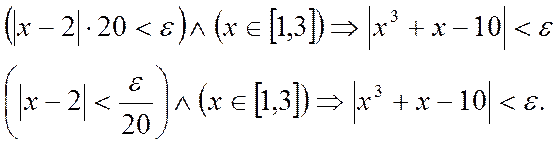
Отсюда, в качестве d можно взять  Число d£1, т.к. xÎ[1,3]. Таким образом, условие ограниченности x2 +2x +5, а следовательно, возможность сведения неравенства ½x3 +x-10½< e к более простому
Число d£1, т.к. xÎ[1,3]. Таким образом, условие ограниченности x2 +2x +5, а следовательно, возможность сведения неравенства ½x3 +x-10½< e к более простому  повлекло за собой ограничение области изменения x, т.е. ограничение на величину d сверху. Если e мало (например, e<1), то
повлекло за собой ограничение области изменения x, т.е. ограничение на величину d сверху. Если e мало (например, e<1), то 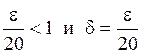 , т.е. ограничение d£1 не является существенным. Далее заметим, что даже при малых e>0 число
, т.е. ограничение d£1 не является существенным. Далее заметим, что даже при малых e>0 число 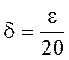 не является наибольшим возможным d(e). Однако, как мы уже отмечали, наибольшее d(e) в определении предела и не нужно.
не является наибольшим возможным d(e). Однако, как мы уже отмечали, наибольшее d(e) в определении предела и не нужно.
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 397; Нарушение авторских прав?; Мы поможем в написании вашей работы!