Моделирование случайных событий

В теории вероятностей реализацию некоторого комплекса условий называют испытанием. Результат испытания, регистрируемый как факт, называют событием.

Случайным называют событие, которое в результате испытания может наступить, а может и не наступить (в отличие от достоверного события, которое при реализации данного комплекса наступает всегда, и невозможного события, которое при реализации данного комплекса условий не наступает никогда). Исчерпывающей характеристикой случайного события является вероятность его наступления. Примерами случайных событий являются отказы в экономических системах; объемы выпускаемой продукции предприятием каждый день; котировки валют в обменных пунктах; состояние рынка ценных бумаг и биржевого дела и т.п.

Моделирование случайного события заключается в " определении ("розыгрыше") факта его наступления.

Для моделирования случайного события А, наступающего в опыте с вероятностью , достаточно одного случайного (псевдослучайного) числа R, равномерно распределенного на интервале [0;1]. В случае попадания ПСЧ R в интервал 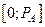событие А считают наступившим в данном опыте; в противном случае — не наступившим в данном опыте. На рис. 1 показаны оба исхода: при ПСЧ 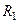событие следует считать наступившим; при ПСЧ — событие в данном испытании не наступило. Очевидно, что чем больше вероятность наступления моделируемого события, тем чаще ПСЧ, равномерно распределенные на интервале [0;1], будут попадать в интервал 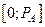, что и означает факт наступления события в испытании.

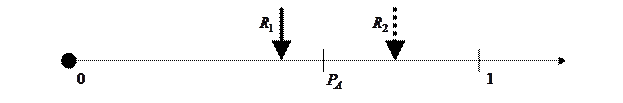
Рис. 1. Моделирование случайных событий.

Для моделирования одного из полной группы N случайных несовместных событий , ,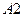…, , 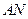с вероятностями наступления 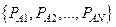соответственно, также достаточно одного ПСЧ R.

Напомним, что для таких случайных событий можно записать:

.

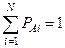Факт наступления одного из событий группы определяют исходя из условия принадлежности ПСЧ R тому или иному интервалу, на который разбивают интервал [0;1]. Так, на рис. 2 для ПСЧ 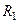считают, что наступило событие А 2. Если ПСЧ оказалось равным , считают, что наступило событие .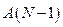

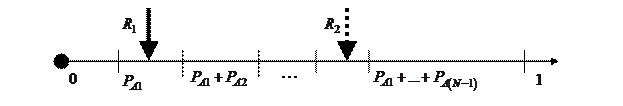
Рис. 2.Моделирование полной группы несовместных событий.

Если группа событий не является полной, вводят дополнительное (фиктивное) событие 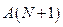, вероятность которого определяют по формуле:

.

Далее действуют по уже изложенному алгоритму для полной группы событий с одним изменением: если ПСЧ попадает в последний, 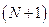-й интервал, считают, что пи одно из N событий, составляющих неполную группу, не наступило.

В практике имитационных исследований часто возникает необходимость моделирования зависимых событий, для которых вероятность наступления одного события оказывается зависящей от того, наступило или не наступило другое событие. В качестве одного из примеров зависимых событий приведем доставку груза потребителю в двух случаях: когда маршрут движения известен и был поставщиком дополнительно уточнен, и когда уточнения движения груза не проводилось. Понятно, что вероятность доставки груза от поставщика к потребителю для приведенных случаев будет различной.

Для того чтобы провести моделирование двух зависимых случайных событий А и В, необходимо задать следующие полные и условные вероятности:

; ; ; .

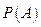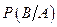Заметим, что, если вероятность наступления события В при условии, что событие А не наступило, не задана, ее можно определить по формуле:

.

Существуют два алгоритма моделирования зависимых событий. Один из них условно можно назвать "последовательным моделированием"; другой — "моделированием после предварительных расчетов".

Дата добавления: 2014-01-07