Моделирование после предварительных расчетов

Последовательное моделирование

Алгоритм последовательного моделирования представлен на рис. 3.

Несомненными достоинствами данного алгоритма являются его простота и естественность, поскольку зависимые события "разыгрываются" последовательно — так, как они наступают (или не наступают) в реальной жизни, что и является характерной особенностью большинства имитационных моделей. Вместе с тем алгоритм предусматривает троекратное обращение к датчику случайных чисел (ДСЧ), что увеличивает время моделирования.

Рис. 3. "Последовательное моделирование" зависимых событий.

Приведенные на рис. 3 четыре исхода моделирования зависимых событий образуют полную группу несовместных событий. На этом основан алгоритм моделирования, предусматривающий предварительный расчет вероятностей каждого из исходов и "розыгрыш" факта наступления одного из них, как для любой группы несовместных событий. Рис. 4 иллюстрирует разбиение интервала [0;1] на четыре отрезка, длины которых соответствуют вероятностям исходов наступления событий.

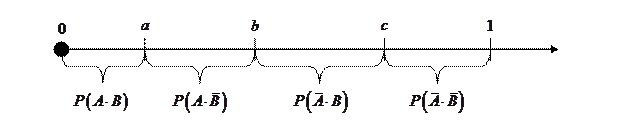
Рис. 4.Разбиение интервала [0;1] для реализации алгоритма

моделирования зависимых событий "после предварительных расчетов".

На рис. 5 представлен алгоритм моделирования. Данный алгоритм предусматривает одно обращение к датчику случайных чисел, что обеспечивает выигрыш во времени имитации по сравнению с "последовательным моделированием", однако перед началом работы алгоритма исследователь должен рассчитать и ввести вероятности реализации всех возможных исходов (естественно, эту несложную процедуру можно также оформить программно, но это несколько удлинит алгоритм).

Рис. 5.Алгоритм моделирования зависимых случайных событий

"после предварительных расчетов".

Дата добавления: 2014-01-07