Метод обратной функции

Моделирование непрерывных случайных величин

Моделирование случайных величин

Технология моделирования случайных факторов

Имитационные модели информационных систем

Лекция №14

Содержание лекции

Имитационные модели информационных систем... 1

Технология моделирования случайных факторов. 1

Моделирование случайных величин. 1

Моделирование непрерывных случайных величин. 2

Метод обратной функции. 2

Метод исключения (Неймана) 3

Метод композиции. 5

Моделирование дискретных случайных величин. 6

Метод последовательных сравнений. 6

Метод интерпретации. 7

Моделирование случайных векторов. 7

Метод условных распределений. 8

Метод исключения (Неймана) 9

Метод линейных преобразований. 10

В практике создания и использования имитационных моделей весьма часто приходится сталкиваться с необходимостью моделирования важнейшего класса факторов — случайных величин (СВ) различных типов.

Случайной называют переменную величину, которая в результате испытания принимает то или иное значение, причем заранее неизвестно, какое именно. При этом под испытанием понимают реализацию некоторого (вполне определенного) комплекса условий. В зависимости от множества возможных значений различают три типа СВ:

§ непрерывные;

§ дискретные;

§ смешанного типа.

Исчерпывающей характеристикой любой СВ является ее закон распределения, который может быть задан в различных формах: функции распределения — для всех типов СВ; плотности вероятности (распределения) — для непрерывных СВ; таблицы или ряда распределения — для дискретных СВ.

Моделирование СВ заключается в определении ("розыгрыше") в нужный по ходу имитации момент времени конкретного значения СВ в соответствии с требуемым (заданным) законом распределения.

Наибольшее распространение получили три метода:

§ метод обратной функции;

§ метод исключения (Неймана);

§ метод композиций.

Метод позволяет при моделировании СВ учесть все ее статистические свойства и основан на следующей теореме:

Если непрерывная СВ Y имеет плотность вероятности , то СВ X, определяемая преобразованием

,

имеет равномерный закон распределения на интервале [0;1].

Теорему доказывает следующая цепочка рассуждений, основанная на определении понятия "функция распределения" и условии теоремы:

.

Таким образом, получили равенство , а это и означает, что СВ X распределена равномерно в интервале [0;1].

Напомним, что в общем виде функция распределения равномерно распределенной на интервале 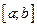СВ X имеет вид:

Теперь можно найти обратное преобразование функции распределения .

Если такое преобразование существует (условием этого является наличие первой производной у функции распределения), алгоритм метода включает всего два шага:

§ моделирование ПСЧ, равномерно распределенного на интервале [0;1];

§ подстановка этого ПСЧ в обратную функцию и вычисление значения СВ Y:

.

При необходимости эти два шага повторяются столько раз, сколько возможных значений СВ Y требуется получить.

Простота метода обратной функции позволяет сформулировать такой вывод: если обратное преобразование функции распределения СВ, возможные значения которой необходимо получить, существует, следует использовать именно этот метод. К сожалению, круг СВ с функциями распределения, допускающими обратное преобразование, не столь широк, что потребовало разработки иных методов.

Метод исключения (Неймана)

Метод Неймана позволяет из совокупности равномерно распределенных ПСЧ , по определенным правилам выбрать совокупность значений с требуемой функцией распределения .

Алгоритм метода

1. Выполняется усечение исходного распределения таким образом, чтобы область возможных значений СВ Y совпадала с интервалом .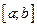

В результате формируется плотность вероятности такая, что

.

Длина интервала 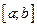определяется требуемой точностью моделирования значений СВ в рамках конкретного исследования.

2. Генерируется пара ПСЧ 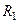и , равномерно распределенных на интервале [0;1].

3. Вычисляется пара ПСЧ и по формулам:

;

,

где .

На координатной плоскости пара чисел определяет точку — например, точку на рис. 1. На рисунке обозначены: А — прямоугольник, ограничивающий график плотности распределения моделируемой СВ; D — область прямоугольника А, находящаяся ниже графика ; В — область прямоугольника А, находящаяся выше графика .

4. Если точка принадлежит области D, считают, что получено первое требуемое значение СВ .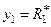

5. Генерируется следующая пара ПСЧ и равномерно распределенных на интервале [0;1], после пересчета по п. 3 задающих на координатной плоскости вторую точку — .

6. Если точка принадлежит области В, переходят к моделированию следующей пары ПСЧ и т.д. до получения необходимого количества ПСЧ.

Рис. 1.Моделирование СВ методом Неймана.

Очевидно, что в ряде случаев (при попадании изображающих точек в область В соответствующие ПСЧ с нечетными индексами не могут быть включены в требуемую выборку возможных значений моделируемой СВ, причем это будет происходить тем чаще, чем сильнее график по форме будет "отличаться" от прямоугольника А. Оценить среднее относительное число q "пустых" обращений к генератору ПСЧ можно геометрическим методом, вычислив отношение площадей соответствующих областей (В и А):

;

;

.

Главным достоинством метода Неймана является его универсальность — применимость для генерации СВ, имеющих любую вычислимую или заданную таблично плотность вероятности.

Дата добавления: 2014-01-07