Линейная зависимость и независимость векторов

Рассмотрим векторы х₁,х₂,…,х_n линейного пространства V. Вектор у=a₁х₁+ a₂х₂ + …+a_nх_n, где a₁,a₂,…, a_n ÎR, называется линейной комбинацией векторов х₁,х₂,…,х_n, а числа a₁,a₂,…, a_n ─ коэффициентами этой линейной комбинацией. Система векторов х₁,х₂,…,х_n называется линейно независимой, если равенство

a₁х₁ + a₂х₂ + …+ a_nх_n = 0 (1)

выполняется только при a₁ = a₂ = … = a_n = 0. Если же существуют числа a₁,a₂,…, a_n не все равные нулю, при которых выполняется равенство (1), то векторы х₁,х₂,…,х_n называются линейно зависимыми.

Из определения нетрудно получить следующие свойства:

1) Всякая система векторов, содержащая нулевой вектор, линейно зависима.

2) Система из одного нулевого вектора линейно независима.

3) Если k из n векторов линейно зависимы, то и вся система из n векторов линейно зависима.

4) Если из системы х₁,х₂,…,х_n линейно независимых векторов отбросить Ã векторов (Ã<n), то оставшиеся векторы также будут линейно независимы.

5) Если в системе векторов имеются векторы х_i и х_j такие, что х_i = ax_j для aÎR, то вся система векторов линейно зависима.

В частности, из свойства 5 следует, что в линейном пространстве R³ любая система векторов, содержащая коллинеарные векторы, будет линейно зависимой.

Теорема 1. Векторы х₁,х₂,…,х_n действительного линейного пространства линейно зависимы тогда и только тогда, когда хотя бы один из них является линейной комбинацией всех остальных.

Доказательство. Пусть векторы х₁,х₂,…,х_n линейно зависимы. Тогда существуют числа a₁,a₂,…, a_n не все равные нулю такие, что

a₁х₁ + a₂х₂ + …+ a_nх_n = 0 (2)

Пусть, например, a_k ¹ 0. Тогда a_kx_k = - a₁x₁ - … - a_k-1x_k-1 - a_k+1x_k+1 - … - a_nx_n и

x_k = - x₁ - … - x_k-1 - x_k+1 - … - 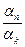x_n,

т.е. х_k ─ линейная комбинация всех остальных векторов.

Пусть теперь один их векторов, например х₁, является линейной комбинацией остальных векторов, т.е. х₁ = a₂х₂ + a₃х₃ + …+ a_nх_n. Тогда (-1)х₁ + a₂х₂ + …+ a_nх_n = 0. Это означает, что векторы х₁,х₂,…,х_n линейно зависимы.

Дата добавления: 2014-01-07