Понятие функции

Предел функции

Лекция 12.

Примеры базисов линейных пространств.

Размерность и базис линейного пространства.

Определение. Число n называется размерностью линейного пространства V, если выполняются следующие условия:

1) в V существует n линейно независимых векторов;

2) любая система n + 1 векторов из V линейно зависима.

Размерность линейного пространства V обозначают dimV = n, то V называют n-мерным линейным пространством. Если пространство состоит из одного нулевого элемента, то его размерность считают равной нулю. Итак, размерность линейного пространства ─ это наибольшее возможное количество линейно независимых элементов в нём.

Базисом n-мерного линейного пространства V называется любая упорядоченная система n линейно независимых векторов этого пространства.

1) Базисом действительного пространства R³ является любая тройка некомпланарных векторов. Базис действительного линейного пространства R² ─ любые два неколлинеарных вектора.

2) Базисом n-мерного арифметического пространства Rⁿ является, например, система векторов

е₁ = (1,0,…,0), е₂ = (0,1,0,…,0), …, е_n = (0,…,0,1).

Функция. Предел функции. Односторонние пределы. Бесконечно большие и бесконечно малые функции.

Математический анализ ─ раздел математики, в котором изучаются функции. Основу математического анализа составляет дифференциальное и интегральное исчисление, теория рядов. Заслуга открытия дифференциального исчисления принадлежит английскому математику и физику Исааку Ньютону (1643 – 1727) и Готфриду Вильгельму Лейбницу (1646 – 1716), немецкому математику и философу.

Понятие функции ─ одно из основных понятий современной математики.

Рассмотрим множество X элементов х и множество Y элементов y. Если каждому элементу хÎΧ поставлен в соответствие единственный элемент уÎΥ, обозначаемый

у = f(x), то говорят, что на множестве Х задана функция у = f(x) со значениями в множестве Y. Элементы хÎΧ называются значениями аргумента, а элементы уÎΥ ─ значениями функции. Множество Х называется областью определения функции, множество всех значений функции ─ областью значений этой функции.

Употребляются следующие обозначения функции: у = f(x), y = F(x), y = Ф(х), у = φ(х) и т.п. Значение, которое функция у = f(x) принимает при х = а, обозначается f(a).

К традиционным основным способам задания функции относятся: аналитический, графический и табличный.

Аналитический способ задания функции ─ это задание функции с помощью формул. Например, у = 2х, у = lgx, у =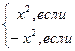

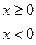
Функция заданная формулой у = f(x), правая часть которой не содержит у, называется явной функцией.

Рассмотрим уравнение F(x;y)=0. Предположим, что существует непустое множество Х значений х таких, что при каждом х₀ÎΧ уравнение F(x₀;y) = 0 имеет действительные решения относительно у. обозначим одно из них через у₀. Сопоставляя таким образом каждому х₀ÎΧ элемент у₀, получим функцию у = у(х), определённую на множестве Х и такую, что F(x;y(x)) º 0 для всех хÎΧ. Функция у = у(ч), определённая таким образом, называется функцией, заданной неявно или неявной функцией.

Например, уравнение 3х + 2у – 5 = 0 неявно задаёт функцию у = − 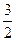х + . Уравнение х² + у² = R² задаёт неявно две функции у = 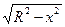и у = − .

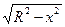Табличный способ задания функции ─ это способ задания функции при помощи таблицы. Примерами такого задания функции являются таблицы тригонометрических функций, таблицы логарифмов и т.д.

Графический способ задания функции ─ это способ задания функции при помощи графика. Графиком функции у = f(x) называется множество точек (x;f(x)) плоскости хОу, где х принадлежит области определения функции. Преимуществом графического способа задания функции является его наглядность.

Если у = f(u), u = φ(х) ─ функции своих аргументов, причём область определения функции у = f(u) содержит область значений функции u = φ(х), то каждому х из области определения функции φ соответствует такое у, что у = f(u), где u = φ(х). Эта функция, определяемая соответствием

y = f(φ(x))

называется сложной функцией или композицией функции φ и f. Например, если у = u², u = sinx, то у = sin²x ─ сложная функция.

Кроме тригонометрических и обратных тригонометрических функций в средней школе изучаются функции: степенная у = х^а (а = const), показательная у = а^х (а = const), логарифмическая у = log_ax (a = const). Все эти функции называются основными элементарными функциями. Элементарными функциями называются функции, которые можно получить из основных элементарных функций с помощью алгебраических действий и образования сложных функций. Например, функции у = lgsinx, y = x² + cosx, y = 3^{lgcosx + sinx} является элементарными.

Дата добавления: 2014-01-07