Диффузионные токи в полупроводниках и диэлектриках

Диффузионный и дрейфовый токи. Соотношение Эйнштейна для коэффициента диффузии носителей заряда в невырожденном полупроводнике. Время релаксации Максвелла. Диффузионная длина. Длина дрейфа. Экспериментальные данные для Ge, Si и GaAs.

Поверхностная рекомбинация. Скорость поверхностной рекомбинации. Эффективное время жизни неосновных носителей заряда. Влияние поверхностной рекомбинации на параметры биполярных приборов и МДП-структур

Статистика рекомбинации через простые рекомбинационные центры (рекомбинационная модель Шокли-Холла-Рида). Время жизни электронно-дырочной пары. Время жизни неосновных носителей заряда. Влияние уровня возбуждения и температуры на времена жизни неосновных носителей заряда. Экспериментальные данные для Ge, Si и GaAs.

Центры рекомбинации и прилипания носителей заряда. Параметры центров рекомбинации и влияние их на время жизни. Изменение избыточной концентрации носителей заряда во времени. Экспериментальное определение времени жизни.

Неравновесная статистика электронов в твердых телах. Неравновесные носители заряда. Генерация и рекомбинация носителей заряда. Уравнение непрерывности. Время жизни неравновесных носителей. Механизмы рекомбинации. Линейная и квадратичная рекомбинация.

Рекомбинация неравновесн. НЗ в полупроводниках и диэлектриках

Неравновесные носители – в состоянии Термодинамического Равновесия в полупроводнике (диэлектриках) непрерывно происходят процессы термической генерации и рекомбинации равновесных носителей. Скорость терм. генерации G₀ равно скорости рекомбинации R₀.

Условию этому соответствует равновесной концентрации n₀p₀=n_i²

Полупроводник (диэлектрик) можно перевести в неравновесное состояние освещением светом с энергией фотонов hv> _ΔEg. При поглощении фотонов происходит генерация дополнительных электронов и дырок к равновесным.

В результате увеличения их концентрации на величины _Δn и _Δp соответственно.

Ошибка: источник перекрестной ссылки не найден

Общая концентрация n=n₀+_Δn

p=p₀+_Δp носит название неравновесной.

_Δn_,Δp – избыточные концентрации

Наряду с оптической генерацией НЗ происходит обратный процесс – рекомбинация энергия рекомбинирующих частиц выделяется в виде фотонов(рекомбинационное излучение) и рекомбинация называется излучательной (люминисцентной) или на нагрев кристалла(возбуждение колебаний кристалл решетки) – Резиизлучательная рекомбинация.

При =R избыт конц _Δn=_Δp

Характеристикой рекомбинации является время жизни неравновесных носителей заряда. –τ.

Носители заряда в полупроводнике (диэлектрике) находящимся в неравновесном. состоянии, называются неравновесными.

Для них np≠n_i² и они подчиняются неравновесной статистике.

Неравновесная статистика.Электронные и дырочные квазиуровни Ферми.

Для нахождения n и p используются те же функции расщепления и формулы для расчета концентраций в равновесном случае. Но вместо уровня F вводят квазиуровни.

Fn – электронный квазиуровня Ферми, Fp – дырочный квазиуровень Ферми.

Неравновесная формула распределения ƒф-0(E,T)=1/(e^(E-F)/kT+1

Неравновесная концентрация электронов n=eNc/√nФ_1/2(ξ*), ξ*= (Fn-Ec)/kT;

для дырок:p=2Nv/√nФ_1/2(η^*), η^*=(Ev-Ep)/kT

для электронов: n=Nc*e^-(Ec-En)/kT = Nc*e^{-(Ec-Fn+F-F)/kT}=n₀e^{-(Ec-Fn+E-F)/kT} =n₀e^(Fn-F)/kT

(Fn-F) определить степень отклонения (уровень инжекции) конц от равновесной.

Квазиуровень Ферми Fn: Fn=F+kTln(n/n₀)

Для дырок p=N_γe^{(-Fp-Ev+F-F)/kT}=p₀e^(F-Fp)/kT

Произведение n*p=n₀p₀e^(Fn-Fp)/kT ≠ n_i²

Время жизни неосновных носителей

Рассмотрим случай линейной рекомбинации, когда скорость носителей пропорциональна их избыточной концентрации – _Δn, _Δp (рекомбинация через примесные центры).

Ошибка: источник перекрестной ссылки не найден

Избыточная концентрация изменяется во времени d(_Δn)/dt=G-R где R=_Δn/τ, 1/τ – вероятность рекомбинации неравновесных носителей в единицу времени.

d(_Δn)/dτ=G-_Δn/τ

В стационарном состоянии d(_Δn)/dτ=0 G=R= _Δn/τ

_Δn=Gτ

т. е. τ определяет изб концентрация e или n

Статистика рекомбинаций через простые рекомбинационные центры

Время жизни неравновесной электронно-дырочной пары (τ_n), время жизни неосновных носителей заряда - τ_n и τ_p

Рекомбинационная модель

Ошибка: источник перекрестной ссылки не найден

Найдем скорости рекомбинации Rn и Rp

Определение Rn – необходимо знать параметры полупроводника и рекомбинационных центров

Nt – концентрация РЦ Et – уровень РЦ

Cn(E) – вероятность захвата электрона одним нейтральным РЦ

Ln(E) – вероятность терм. Возбуждения захваченных электронов с уровнем Еф в ЗР

ƒt – функция распределения электронов по ур Et

ƒn – неравновесная функция реакция e в зоне проводимости

Рассмотрим изменение концентрация электронов в интервале E, EtdE в ЗП в результате захвата РЦ и их терм возбуждения.

dr_n~число е, захват РЦ в единицу времени (Vкрист=1)

dqn-“-“ – возбуждение в ЗП с Ур Ei

dRn=dr_n - dq_n - изменение числа е в ЗП в интервале dE в результате рекомбинации или d/Rn – элементы скорости рекомбинации.

Время жизни электронно-дырочной пары (τ_n)

τ_n, τ_n,p определяется из скорости объемных безизлучательной рекомбинации R

Вычислим элементарную скорость рекомбинации dRn для электронов, захваченных из зоны проводимости из интервала энергии E, E+dE с учетом вероятностей C_n(E) и ln(E) и функцией распределения ƒn иƒt

Число е, захваченных в единицу времени: dr_n=Cn(F)ƒnN(E)dE(1-ƒ)N(t)

Часть захваченных е возбуждается обратно в ЗП с Ур Et

dq_n = ln(E)Niƒt(1-ƒn)N(E)dE

Тогда dR_n=dr_n-dq_n

drn= [Cn(E) ƒn(1-ƒt)-ln(E) ƒt(1-ƒn)]Ntdt

Полная скорость рекомбинации электронов:

Rn=₀∫^∞dRn

Для скорости рекомбинации дырок Rp расчет аналогичен. Необходимо вероятность захвата дырок Cp(E) рекомбинационных центром и вероятность возбуждения дырок lp(E) в ВЗ

dRp=dr_p-dq_p, Rp = ₀∫^∞dRp

Для данной рекомбинационной модели

Rn=_Δn/τ_n; Rp= _Δp/τ_{p Δ}n,_Δp – избыточные концентрации

Поскольку _Δn=_Δp и Rn=Rp то τ_n= τ_p

Время жизни e-n пары в этой статистике рекомбинации равно:

1)τ_n= τ_p*[(n₀+n₁+_Δn)/(n₀p₀+_Δn)]+τ_n0[(p₀+p₁+_Δp)/n₀+p₀+_Δn)]

τ_p0=1/SpNtVтепл – min время жизни дырок п.п n-типа когда РЦ полностью заполнена e

n₁=Nc*e^–(Ec-Et/kt – т е концентрация электронов при условии F=Et

τ_n0 = 1/(SnNtV) – min время жизни в полупроводнике р-типа

Выражение 1) для τ_n позволяет исследовать влияние на τ_n ур инжекции(_Δn,_Δp), легирования и параметров рекомбинационных центров при разных t⁰.

Влияние легирования (поглощение ур Ферми) на τ_р при низком уровне инжекции

_Δn<<n_{0 Δ}p<< p₀

2) τ_n= τ_p*[(n₀+n₁)/(n₀p₀)]+τ_n0[(p₀+p₁)/(n₀+p₀)]

Для анализа выражения 2) для ТП ЗЗ _ΔEg разделим на области

n-тип Ei<F<Ec – сильнолегированный п/п p-типа

Область Et<F<Ec: n₀>>p₀

n₁>>p₁

n₀>>n₁

Для τ_n получим: τ_n~τ_p0 т.о.время жизни (e-h) пары = min времени жизни неосновных носителей заряда.

n-тип область Ei <F<(Ec-Et) – слаболегированный полупроводник n-типа

n₀>>p₀ n₀<<n₁

τ_n~ τ_p0(n₁/n₀) т е τ_n зависит от n₀ (уровня легирования)

τ_n возрастает т к n и n₀ зависят от Т след τ_n тоже

n₁/n = (Nc(T)e^-(Ec-Et)/kT)/(Nc(T)e^-(Ec-F)/kT)= e^-(Et-F)/kT

τ_p0 – слабо легированный от Т

Полупроводник р-типа

Сильнолегированный τ_n~ τ_p0

Слаболегированный τ_n~ τ_p0*p₁/p₀

Сильный уровень инжекции

_Δn>>n_{0 Δ}p>> p₀

τ_n∞= τ_p0 + τ_n0 т е определяется параметрами центров рекомбинации и не зависит от равновесных конц n₀ и p₀

Раздел 6. Диффузия и дрейф неравновесных носителей заряда

6.1. Диффузионный и дрейфовый токи. Соотношение Эйнштейна для коэффициента диффузии носителей заряда в невырожденном полупроводнике. Время релаксации Максвелла. Диффузионная длина. Длина дрейфа. Экспериментальные данные для Ge, Si и GaAs.

6.2. Биполярный коэффициент диффузии, дрейфовая подвижность и диффузионная длина. Экспериментальные данные для Ge, Si и GaAs. Движение неравновесных носителей заряда в электрическом поле. Длина затягивания по полю и против поля. Инжекция, экстракция, аккумуляция и эксклюзия неравновесных носителей заряда.

Распределение избыточных концентраций неравновесных носителей во времени и пространстве (объеме образца)

В общем случае неравновесные конц носителей зависят от корд и времени, т е n=n(r,t) и p=p(r,t)

Для нахождения их распредления используется уравнение непрерывности

Уравнение непрерывности

Вводит на основании Уравнения непрерывности из электродинамики: ∂ρ_g/∂t +diVj=0 (1)

ρ_g – объемная плотность электрического заряда

j- плотность электрического тока

В проводимой среде объемный заряд не накапливается (рассасывается) в результате расходимости тока

В уравнении (1) введем процессы генерации и рекомбинации носителей.

Уравнение непрерывности для электронов:

∂(_Δn)/∂t = -1/q_n(diV jn)+Gn-Rn

Т е число e в данном V изменяется в результате переноса заряда (дрейф и диффузия), генерации и их рекомбинации.

j_n=j_dn-j_Pn

Для дырок: ∂(_Δp)/∂t = -1/(qp)(d,Vj_p)+Gp-Rp

j_p= j_dn+j_Pn

Если ∂(_Δn)/∂t=0 или: ∂(_Δp)/∂t=0 – имеем стационарное состояние

В металлах диффузионные токи не существуют из-за высокой равновесной концентрации электронов. Диффузионные токи возникают при неравномерном освещении полупроводника

В освещенной части образца концентрация электронов >, чем в затемненной, - возникает градиент концентраций в результате чего электрон из левой части будет диффузировать в правую часть.

Аналогично - для дырок. Диффузия приводит к возникновению направленных потоков зарядов, т е возникает диффузионный ток.

Одномерный случай: вычислим jp_n :

jp_n = -q_n*Dn*d(_Δn)/dx=qDn d(_Δn)/dx

Dn- коэффициент диффузии неравновесных e

Для дырок: j_Dp=-q_pD_pd(_Δp)/dx=-qDpd(_Δp)/dx

Коэффициент Dn и Dp определяют из соотношения Эйнштейна D=kT/q*μ

Объемный случай:

j_Dn= qD_nD_rn(r)

j_Dp= -qD_pD_rp(r)

Распределение избыточной концентрации неосновных носителей во времени. Время жизни неосновных носителей

Образец полупроводника n-типа при стационарном и импульсном освещении.

Стационарное освещение: в образце однородно возбуждается неравновесные носители

Рассмотрим низкий уровень возбуждения _Δn<<n₀ n₀>>p_{0 Δ}p>> p₀

n₀, p₀ - равновесные концентрации

В этих условиях сильно изменяются и концентрации дырок (_Δp>> p₀) – т е неосновных носителей

Найдем _Δp из уравнения непрерывности: d(_Δp) из уравнения непрерывности:

d(_Δp)/dt=-1/q div jp+Gp-Rp

jp=0 т к нет диффузии и дрейфа дырок d(_Δp)/dt=0, т к в условиях стационарного освещения _Δp не зависят от t

Gp-Rp=0, Gp=Rp процессы генерации и рекомбинации уравновешивают друг друга

В этом случае _Δp= _Δp_стац – стационарное значение избыточной концентрации дырок в полупроводнике n-типа

_Δp_стац = -Gp*τ_p (Rp= _Δp/Dp)

Импульсное освещение

Образец n-типа освещается прямоугольным импульсом света длительностью _Δt>>τ_p

_{Ошибка: источник перекрестной ссылки не найден}

Найдем _Δp(t) при выключении света уравнение непрерывности d(_Δp)/dt=- _Δp/τ_p (Gp=0)

_Δp(t)=p_стац*e^-t/τp

Где _Δp_стац=_Δp(0)

Время жизни неосновных носителей заряда в полупроводнике р-типа:

Низкий уровень инжекции

_Δp<< p₀ n₀<<p_{0 Δ}n>>n₀ т.е. сильно изменяется концентрация электронов – неосновных носителей заряда в р-типе. Концентрация основных носителей заряда не изменяется. При стационарном освещении _Δn_стац = G_nτ_n где τ_n время жизни электронов в р-типе.

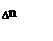
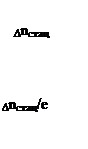При импульсном освещении: _Δn(t)= _Δn_стац*e^-t/τn Ошибка: источник перекрестной ссылки не найден

Т о τ_n – время, в течение которого избыточная концентрация _Δn уменьшается в е-раз в результате рекомбинации.

Распределение избыточной концентрации неосновных носителей заряда в пространстве

Найдем распределение _Δp(x) в образце n-типа при отсутствии электрического поля (E=0) – диффузионное приближение в сильном ЭП.

Дифуззионное приближение. Диффузионная длина неосновных носителей.

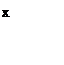
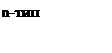
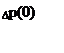
При х=0 – инжектирующая плоскость – вводим стационарно дырки в концентрации _Δp(0)

Определим _Δp(х) в условиях диффузии и рекомбинации: ∂(_Δp)/∂t=-1/q div j_pD-_Δp/τ_p

В этом случае ∂(_Δp)/∂t=0: j_pD=-q_Dp∂(_Δp)/∂x

Dp div (∂(_Δp)/∂x)-_Δp/τ_p=0

∂²(Δp)/∂x² – _Δp/ τ_p D_p=0

Введем величину Lp²=D_pτ_p

∂²(_Δp)/∂x² – _Δp=0

Граничные условия: _Δp(x)|_x→∞=0(p=p₀)

_Δp(x)|_x=0=_Δp(0)

Т е _Δp(x) убывает с расстоянием в результате рекомбинации дырок

Общее решение: _Δp(x)=A*e^x/Lp+B*e^-x/Lp

A=0 из граничных условий

D= _Δp(0)

Т е _Δp(x)= _Δp(0)e^-x/Lp – избыточная концентрация неосновных носителей заряда – дырок в образце n-типа

Спадает по exp-закону с характер. Длиной

Lp=√D_pτ_p Lp-диффузионная длина дырок – расстояние на котором _Δp(0) уменьшается в е раз, или расстояние которое проходят дырки в образце n-типа за время их жизни

Ошибка: источник перекрестной ссылки не найден

Для электронов в р-типе

_Δn(x)= _Δn(0)e^-x/Ln

Где Lp=√D_pτ_p для линейной рекомбинации

Дата добавления: 2014-01-07