Разработка управленческого решения

Электронно-дырочный переход. Явления инжекции и экстракции. Теория выпрямления электронно-дырочного перехода, емкость р-n перехода. Биполярные приборы микроэлектроники с р-n переходами. Гетеропереходы. Типы гетеропереходов. Построение энергетической диаграммы гетероперехода. Электрические свойства гетеропереходов. Основные гетеропереходные пары. Приборы с гетеропереходами. Сверхрешетки. Приборы на сверхрешетках. Варизонные структуры и область их применения.

Термоэлектронная и фотоэлектрическая работа выхода. Контактная разность потенциалов. Потенциальные барьеры в контакте металл-полупроводник (модель Шоттки). Распределение концентрации электронов и потенциала в слое объемного заряда. Выпрямление в контакте металл-полупроводник. Вольт-амперная характеристика. Диодная и диффузионная теория выпрямления. Вольт-фарадная характеристика. Диод Шоттки. Омический контакт. Определение высоты барьера Шоттки на контакте металл-полупроводник. Высота барьеров, наблюдаемых у различных полупроводников. Влияние поверхностных состояний на высоту барьера. Приборы с барьером Шоттки в микроэлектронике.

Биполярный коэффициент диффузии, дрейфовая подвижность и диффузионная длина. Экспериментальные данные для Ge, Si и GaAs. Движение неравновесных носителей заряда в электрическом поле. Длина затягивания по полю и против поля. Инжекция, экстракция, аккумуляция и эксклюзия неравновесных носителей заряда.

Биполярная диффузия. Биполярная диффузионная длина

При освещении образца полупроводника ростом из области сильного поглощения генерируются е и n вблизи освещенной поверхности – возникает градиент концентраций е и по отношению к неосвещенной поверхности.

e и n диффузируют в объем образца при этом е упрежают дырки(т к μ_n>μ_p) что приводит к возникновению ЭП E_D, которое ускоряет дырки- происходит совместная диффузия е и n – биполярная диффузия, которая характеризуется биполярным коэффициентом диффузии – D и биполярной диффузионной длиной L

D=(n+p)/(n/Dp+p/Dn) или D=(n₀+p₀)/(n₀/Dp+p₀/Dn) – для низкого уровня инжекции

Образец n-тип n0>>p0

D=Dp – т о биполярный коэффициент D определяет коэффициент Диффузии неосновных носителей заряда Dp

p-тип D=Dn

Собственный п/п D=2n_iDnDp/n_i(Dn+Dp)=2DnDp/(Dn+Dp)

Ошибка: источник перекрестной ссылки не найденБиполярная диффузионная длина L=√Dτ_пары

Диэлектрическое время релаксации-τ_n

Среднее время жизни объемного заряда неравновесных носителей – объемный заряд исчезает в результате проводимости: ∂ρ_g/∂t = - div jd

Id=σE div jd=div(σE)=(divσ)E+σdivE

div jd= σdivE

divE=4π*ρ_g/E

т о ∂ρ_g/∂t=-4πσ/E* ρ_g Введем τ_m=E/4πσ

о ∂ρ_g/∂t=-ρ_g/ τ_m ρ_g(t)= ρ(0)e^-t/tm

ρ(0)=- ρ(t) t=0

Т о объемный заряд основных носителей заряда ρ_g сгорает по exp-закону с характеристическим временем

τ_m=E/4 πσ

τ_m<< τ_n,τ_p

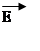
Ошибка: источник перекрестной ссылки не найден

Если вводим ρ_g слева то справа через τ_n такой же заряд ρ_g должен уйти из образца в цепь через время τ_m

Дрейфовая длина неосновных носителей

Найдем распределение Δp(x) в n-типе в условиях сильного поля (диффузии нет)

∂(_Δp)/∂T=-1/q div jp_d- _Δp/τ_p; ∂(_Δp)/∂T=0

1/q div jp_d+_Δp/τ_p=0

div j_pd=div(qpμ_p)E=qμ_p∂p/∂xE+qμ_pp*divE

1/q div jp_d=μ_p∂p/∂xE

p(x)=_Δp(0)e^-x/e

Дрейфовая длина неравновесных дырок (lp) в полупроводнике n-типа

Определим из уравнения непреывности при условии E≠0, дир. Jp_d=0

∂(_Δp)/∂x- _Δp/(μ_pEτ_p)=0 Обозначим lp=μ_pEτ_p

∂(_Δp)/∂x-_Δp/lp=0

lp – расстояние которое проходят неравновесные дырки со скоростью дрейфа

_Δp(x)= _Δp(0)*e^-x/lp

_Δp(x) – убывает с расстоянием от плоскости инжекции х=0 по экспоненте.

Инжекция и экстракция неравновесных носителей

Инжекция – обогащение объема полупроводника неравновесными неосновными носителями при наложении электрического поля на полупроводник.

Экстракция - обеднение

τ_μ<<τ_n τ_ρ

ē

^јd

Объёмный заряд основной носитель заряда вводится при пропускании тока через образец.

Если вводим ρ_q слева, то справа через τ_μ такой же заряд ρ_q должен уйти из образца в цепь через время τ_μ

Дрейф неосновных носителей

Найдём распределение ∆ρ(х) в n-типе в условиях сильного поля (диффузии нет)

;

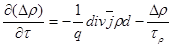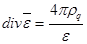
Дрейфовая длина неравновесных дырок (е_ρ) в полупроводниках n-типа

Определить из уравнения непрерывности, при условии 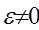, div(j_ρ)=0

Обозначаем:

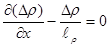
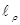-расстояние, которое проходят неравновесные дырки со скоростью дрейфа

за время жизни

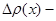убывание с расстоянием от площадки инжекции х=0 по exp

Инжекция и экстракция неравновесных носителей

Инжекция- обогащение объёма полупроводника неравновесными не основными носителями наложений электрического поля на полупроводник

Экстракция- обеднение

Полупроводник n-типа:

Поверхностная рекомбинация не основных носителей

На поверхности реальных кристаллов имеются центры рекомбинации в объёме, которые эффективно уменьшают время жизни 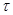и избыточную концентрацию 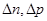в приповерхностном слое.

Рекомбинационные свойства поверхности оценивают темпом поверхности рекомбинации U_s (количество носителей заряда, которые рекомбинируют на единицу поверхности в секунду) и скорость поверхности рекомбинации S

S связывает U_s с избытком концентрации неравновесных носителей

Us=S 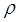(для объёмности рекомбинации) 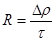S-зависит от качества обработки поверхности, для свежесколотой поверхности S=0

Поверхностное время жизни 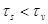(объёмное), поэтому рекомбинационные свойства кристалла оценивают эффективным временем жизни

.

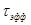Распределение избыточной концентрации при поверхностной рекомбинации

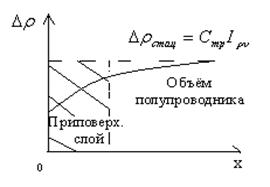
-уменьшается при х=0, поэтому к поверхности будет направлен поток дырок

-D/_х=0=U_s пока есть неравновесные дырки в объёме

Коэффициент инжекции

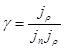отношение плотности тока не основных носителей заряда к суммарному току через полупроводник.

Используют для оценки инжекционных свойств контактов.

Раздел 7. Контактные явления

7.1. Термоэлектронная и фотоэлектрическая работа выхода. Контактная разность потенциалов. Потенциальные барьеры в контакте металл-полупроводник (модель Шоттки). Распределение концентрации электронов и потенциала в слое объемного заряда. Выпрямление в контакте металл-полупроводник. Вольт-амперная характеристика. Диодная и диффузионная теория выпрямления. Вольт-фарадная характеристика. Диод Шоттки. Омический контакт. Определение высоты барьера Шоттки на контакте металл-полупроводник. Высота барьеров, наблюдаемых у различных полупроводников. Влияние поверхностных состояний на высоту барьера. Приборы с барьером Шоттки в микроэлектронике.

7.2. Электронно-дырочный переход. Явления инжекции и экстракции. Теория выпрямления электронно-дырочного перехода, емкость р-n перехода. Биполярные приборы микроэлектроники с р-n переходами. Гетеропереходы. Типы гетеропереходов. Построение энергетической диаграммы гетероперехода. Электрические свойства гетеропереходов. Основные гетеропереходные пары. Приборы с гетеропереходами. Сверхрешетки. Приборы на сверхрешетках. Варизонные структуры и область их применения.

Контактные явления -физические явления которые возникают в структурах с контактными (_M/_M, _M/n, n/n)

Основные понятия физики контактов

Зонные модели М и П

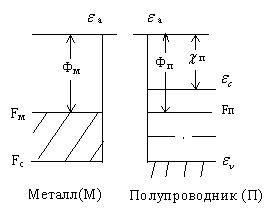
-уровень вакуума (начало отсчёта энергии), уровень на котором кинетическая энергия ē=0

Ф_м и Ф_п – терм. Работы выхода электрона из М и П- энергия, которую нужно сообщить электрону для его перевода с уровня Ферми на уровень

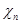- энергия электронного сродства – внешняя (фотоэлектрическая) работа выхода- энергия, необходимая для перевода электрона с уровня на уровень

Токи термоэлектронной эмиссии

Использование в эмиссионной модели контактов

Метан: j_тэм=AT²e^-Фμ/кт

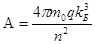^{-const Больцмана}

Полупроводник: j_тэп=А^*Т²е^-Фп/кт

(в А^* вместо m₀→m*_n)

Контакт полупроводника с металлом

Выпрямляющий контакт: М/П (n-типа), если Ф_п<Ф_м -нелинейное вольтамперная характеристика (диод)

Невыпрямляющий контакт - линейка ВАХ (М/П(n-тип) – Ф_п > Фм)

Выпрямляющий контакт

М/П (n-тип) Ф_п < Ф_м

-х=0 –граница контакта

-уровни f_м и f_п при контакте выравниваются из-за обмена электронами между М и П

Зонная модель

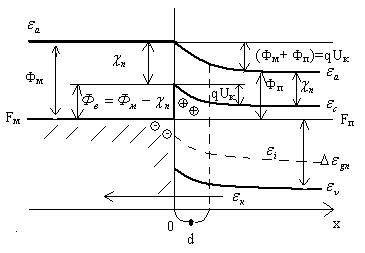
Так как Ф_п<Ф_м при контакте электронов из П уходят в М и образуется двойной объёмный заряд: в П (ионы доноров D⁺) в область толщиной d и заряд на поверхности М (поверхностный d≈0)

d- толщина области объёмного заряда (ТООЗ) контакта М/П (n-типа)- слой повышенного сопротивления (R_{контакта}>R_объёма)

Происходит искривление зон полупроводника вверх на величину qU_к=Ф_м-Ф_п , где - контактная разность потенциалов.

Этот барьер препятствует уходу электронов из П в М, а со стороны М- возникает барьер , препятствующий переходу электронов из М в П.

В равновесии потоки электронов уравновешивают друг друга и ток через переход=0 (j=0)

Нарушить равновесие можно, если приложить внешнее напряжение U, которое изменит барьер q(U_k±U), так как напряжение в структуре в основном падает слой с сопротивлением R_k

Распределение электростатического потенциала 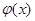и концентрации n(х) для выпрямляющего контакта М/П.

Используя уравнение Пуассона:

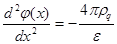; -объёмный заряд в области контакта

=q(-n(x))=q(Nd-n(x))=q(-n(x))

Граничные условия:

x=0 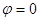n=n₀ - концентрация электронов при х=0 (Граница)

х→∞ φ=U_к n=n₀ (Объём полупроводника)

n(x)=n_к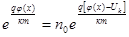

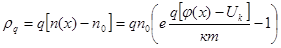
• Случай слабого искривления зон: q<<1

Обозначим: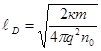

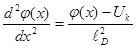
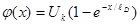-спадает по экспоненте.

- длина экранирования- глубины проникновения электрического поля в объём полупроводника.

• Случай сильного искривления:

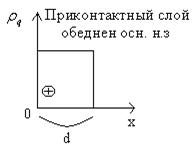
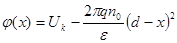
При: х=0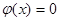

U=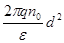 d=- толщина обедненного слоя

ВАХ выпрямляющего контакта М/П (n-типа)

Зонная модель контакта в равновесии (внешнее напряжение U=0)

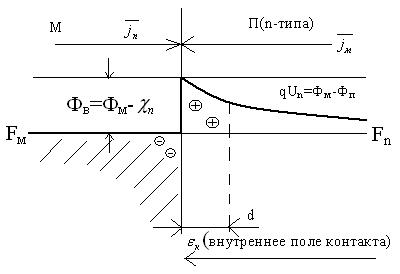
В результате обмена электрополями м/у М и П из П в М течёт ток , а из М в П→ток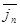

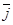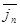= -, j_n=j_м=j₀ -при равновесии потоков электронов (F_м=F_n) токи равны

• Прямая ветвь ВАХ - зависимость прямого тока через контакт j_пр от внешнего напряжения – U

Полезность прямого смещения:

но П (n-типа)) внешнее U падает на обедненное П,

но М) сопротивление которого R_к<R объёма полупроводника

Зонная модель контакта при прямом смещении

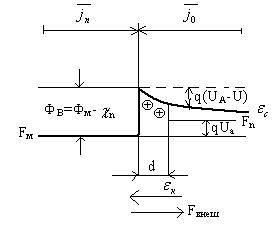
Равновесие нарушается, уровень F_n может выше F_м на величину qU_а –энергии электрона во внешнем поле

Барьер дна электронов из П в М уменьшается- ток j_n возрастает (j_n>j₀), а так 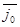=j_м – не уменьшается- внешнее U не влияет на высоту барьера Ф_в

Плотность прямого тока:

j_пр=j_n-j₀=j₀-j₀=j₀(-1)

j_пр=j₀(-1) -прямая ветвь ВАХ ток ↑ с U и зависит от Т

Обратная ветвь ВАХ j_обр=f(Uобр)

Зонная модель контакта при обратном смещении

Полярность обратного смещения

Барьер для электронов, выходящих из П в М возрастает на величину qU ток из П в М-j_n уменьшается, а ток j₀-не измениться.

Обратный ток: j_обр=jn-jм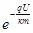=j₀-j₀

Обратная ветвь ВАХ j_обр=j₀(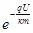_-1)

Ток при малых U~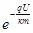_, а при больших j_обр=j₀ – ток насыщения контакта.

ВАХ выпрямляющего контакта

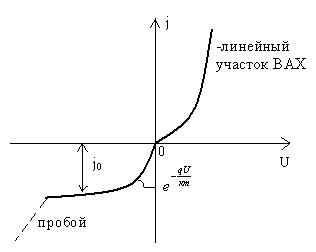
При больших прямых смещениях барьер исчезает и контакт становится невыпрямляющим- омическим с линейным ВАХ.

При больших обратных напряжениях (U<0) наступает резкое возрастание тока- пробой контакт- вплоть до разрушения

Реальная ВАХ: j=j₀(-1)

U>0- прямой ток

U<0 – обратный

U>(1-2) – возникает из-за туннельных токов (электроны проходят через барьер, а не над барьером) и рекомбинации электронов в области ОЗ

p-n-переход

- структура полупроводника, состояние из контактирующих n и p областей кристалла

Резкий эксцентричный p-n-переход (N_A>N_d)

Х=0 – металлургическая граница

При контакте n и p- областей происходит обмен носителями: электроны переходят в р – область, дырки в n – область. Возникает объёмный заряд 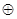в n – области; в p – области.

Распределение концентрации в p-n- перехода

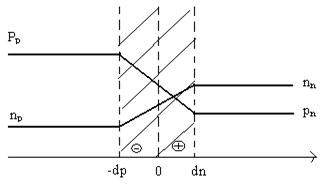
n_n, p_p – концентрация основных носителей заряда

n_p, p_{n –} концентрация не основных носителей заряда

d_n и d_p – толщина 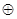и объёмных зарядов в n и p- областей.

ТООЗ d=d_n+d_p – область сильного изменения концентрации носителей – есть физический p-n- переход.

Зонная модель p-n перехода в равновесие

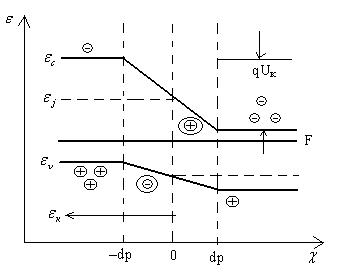
U_к-контактная разность потенциалов

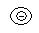ионы доноров; ионы акцепторов; электроны;дырки

Контактная разность потенциалов

U_к возникает в результате диффузионного перераспределения электронов и дырок

U_к=? n_np_p= n_np_p=

n_i-собственная концентрация не основных зарядов U_к=

Толщина объединённого слоя (ТООЗ)

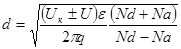
Для резкого ассимметричного p-n перехода

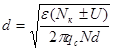
Ёмкость p-n – перехода

p-n – образует плоский конденсатор пластины –более низкоомные р и n области, прилегающие к границам p-n- перехода, диэлектрик - обеднённый слой.

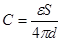S-площадь p-n – перехода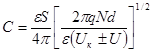

•прямое напряжение: U>0 d↑ C↓ повышение U

•обратное: U<0 d↓ C↑

Вольт-фарадная характеристика p-n – перехода (ВФХ)

Зависимость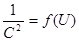

Из ВФХ определяем U_к

Вольт-фарадный метод определения концентрацией примеси.

Из измерения ёмкости p-n – перехода можно определить концентрацию примеси

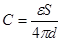
Перенос заряда в p-n –переходе

Прямое смещение- источника напряжена n-областьисточник напряжения на р- области

Зонная модель p-n- перехода

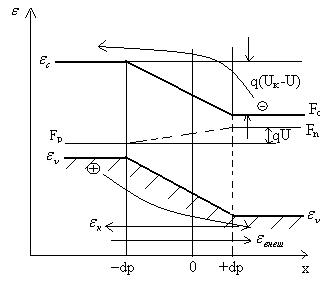
-уменьшает контактную разность потенциалов, барьер p-n – перехода уменьшается на величину qU –термодинамическое равновесие нарушается следовательно происходит инжекция электронов в р – область, дырок в n- область, через p-n – течёт прямой электрический ток, образованный основными носителями.

Обратное смещение - на n – область; на p-область

-внешнее электрическое поле совпадает по направлению с внутренним полем p-n – перехода.

Зонная модель p-n – перехода

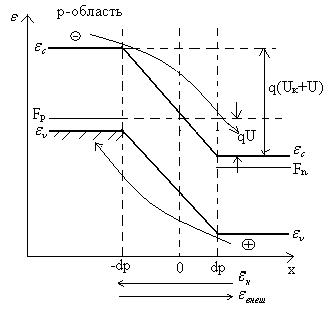
Потенциальный барьер p-n – перехода увеличивается на qU –происходит перенос не основных носителей через p-n – переход:

• дырок из n – области в p - область

• электронов из p – области в n – область

Возникает обратный ток, образованный не основными носителями.

Плотность прямого и обратного тока зависит от приложенного напряжения

j=j_s(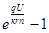) U>0 – прямое смещение; U<0 – обратное

j_s- ток насыщения (имеет диффузионную природу)

j_s=q()

L_n, L_{p –} диффузионная длина D_n, D_p- коэффициент диффузии n_p, p_n – концентрация не основных носителей в р и n – областей p-n – перехода соответственно

При прямых смещениях n>>кт/q барьер p-n – перехода уменьшается (снимается) и прямой ток линейно зависит от U

При обратном смещении U>кт/q обратный ток достаёт насыщения: j_обр=j_s и в дальнейшем может произойти резкое возрастание j_обр – возникает при высоких обратных напряжениях.

При высоких обратных напряжениях возникает разное возрастание обратного тока (j_обр>>J_s) – явление пробоя p-n - перехода может быть обратимым и необратимым.

Омический контакт

М-П (n- тип), Ф_м<Ф_п

Зонные модели М и П до контакта

Зонная модель омического контакта

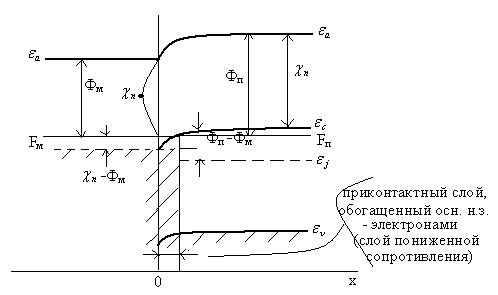
Так как Ф_м>Ф_n, то при контакте электроны из М перейдут в П, а на границе контакта возникает в объёме П – слой, обогащённый основным носителем; сопротивление этого слоя R_конт меньше сопротивления объёма П.

Происходит искривление зон П – вниз. Внешнее напряжение будет падать на объёме П (R_n>>R_к), поэтому так через контакт будет – линейная функция от U (как для омического сопротивления)

Гетеропереходы (ГП)

- контакты П с разными запрещёнными зонами.

Различают классические гетеропереходы (квантово-размерные структуры)

Классические ГП - полупроводники, структуры на трёх мерном электроне, газе;

Нано ГП – на низкомерном электроне, газе.

Классический анизотипный переход

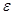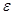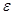- контакт широкозонного полупроводника n –типа (∆dn) с полупроводником p –типа (∆dp<∆dn)

n и p – полупроводник до контакта

∆+∆=- ∆=- ∆=(-)=∆

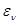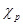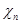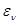ГП в равновесии (U=0)

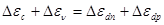
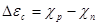
При контакте – в результате обмена носителями → Fn = Fp и происходит искривление зон:

в n-типе: вверх

в p-типе: вниз.

В зоне проводимости структуры возникает разрыв, равный ∆Ec – барьер для электронов,

а в валентной зоне – разрыв - ∆Ev – барьер для дырок.

В состоянии равновесия ток равен нулю через переход, между n- и p- области полупроводников возникает диффузионная потенциал:

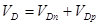
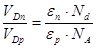, где ε – диэлектрическая проницаемость, Nd и Nа – концентрация доноров в n – полупроводника и акцепторов в p – полупроводника.

Отличия p-n гетероперехода.

потенциальные барьеры для электронов и дырок – различные.

При прямом смещении – возникает явление односторонней инжекции электронов в p-обл., инжекции дырок – не происходит, т.к. барьер для дырок значительно больше, чем для электронов – это улучшает характеристики приборов.

Прямое смещение

«-» -на n-обл. «+» - на p-обл.

Поверхностные электронные состояния, их влияние на контактные явления.

Поверхностные состояния возникают на поверхности кристалла из-за обрыва связи кристаллической решетки и адсорбций примеси на поверхности и слое.

Поверхностные состояния, возникающие из-за обрыва, наз. собственными, и они образуют 2-х мерные энергетические зоны, которые накладывают на объемные зоны кристалла, а также на з.з. Энергия электронов определяется компонентами квазиимпульса P_║, параллельными поверхности (если поверхность при x=0, то – Py и Pz).

Несобственные поверхностные состояния образуют поверхностные примесные центры – им соотв. дискретные уровни Es.

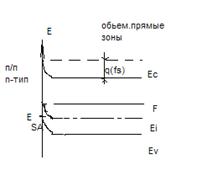
Зонные модели полупроводников с поверхностными состояниями

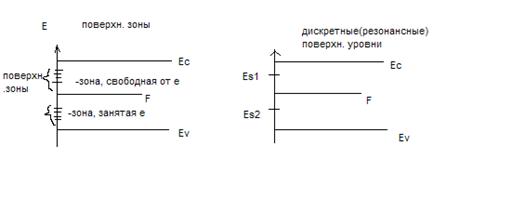
Поверхностный потенциал φ_S

Поверхностные состояния действуют на акцепторы или доноры.

Полупроводник n-типа

ПС – акцептор (ненасыщенная оборванная связь)

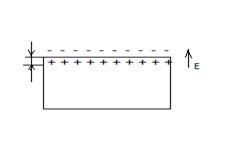
ПС – акцептор забирает электрон из приповерхностного слоя полупроводника – вследствие чего образуется «-» заряд на поверхности и «+» заряд в объеме полупроводника.

Двойной слой заряда приводит к возникновению электрического поля Е и электрического потенциала - поверхностный потенциал = разности потенциалов между поверхностью и объемом.

Глубина проникновения электрического поля = глубине экранирования:

Энергетические зоны (уровни Е_С и Е_V) будут искривлены вверх:

E_C0, E_V0 – уровни в объеме.

Таким образом приповерхностный слой будет обеднен основными носителями заряда и будет иметь проводимость ниже, чем объём.

ПС – донор – приповерхностный слой, обогащается основными носителями заряда и имеет повышенную проводимость

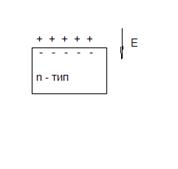
Т.о. ПС изменяют проводимость поверхности и искривляют энергетические уровни. Следовательно, будут влиять на явления в контактах.

Поверхностный потенциал

,

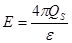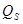- плотность поверхностного заряда,

=

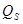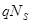
- плотность поверхностных состояний

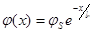- изменение электрического потенциала в приповерхностном слое

Поверхностная проводимость:

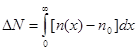
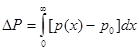
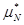- избыточная проводимость, рассчитанная на единицу поверхности.

и - подвижности в приповерхностном слое

Эффект поля

- изменение 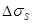под действием внешнего поля.

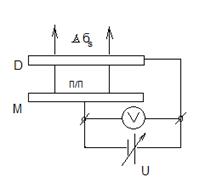
П/п помещают в конденсатор, на который подают внешнее напряжение U, что изменяет Q_S и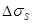

Эффект используют для исследования поверхностных состояний

Влияние ПС на контактную разность потенциалов в структурах с барьером.

При большой плотности состояний они концентрируются вблизи середины запрещённой зоны

И фиксируют уровень ферми вблизи ур Ei

Это приводит к тому что контактная разность потенциалов не зависит от типа проводимости полупроводника и природы металла

НАНОГЕТЕРОПЕРЕХОД

на двухмерном электронном газе

- квантово размерные структуры на ультратонких ⁿ/_n слоях (толщина слоя сравнима с длиной волны Де-Бройля электронного (дырочного) газа, которая составляет в твердом теле нанометры.

Квантование энергии электронов и дырок в полупроводнике

Ультратонкий слой

Размер ⁿ/_n ограничен в направлении z - электронов не могут свободно двигаться в этом направлении, а в плоскости XY ведут себя как свободные электроны с массой m*

Ограничение движения электронов по оси z – приводит к образованию двух бесконечных потенциальных барьеров U_D, расположенных на расстоянии Lz

Поэтому электроны (Блоховские) волны будут отражаться от барьеров, и электроны будут соответствовать не бегущие, а стоящие волны.

Стоячим волнам соответствуют компоненты волн. В.

K_Zn = 2П/λ_ll = П/L_z• n

n = 1 – основное состояние электронов в Я

Значению K_Z (n = 1) соответствует изменению энергии

ẽ: ∆E = ђ²/2m* (П/ L_z)² – это энергия размерного квантования или квантово измерения эффективности

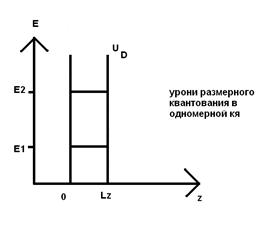
Энергетический спектр двумерного электрона - газа (2∆)

Е (n, k_x, k_y) = E_n + ђ²/2m^x(k_x² + k_y²)

E_n = ђ²/2m^x (П/Lz•n)²

2D – наногетеропереход

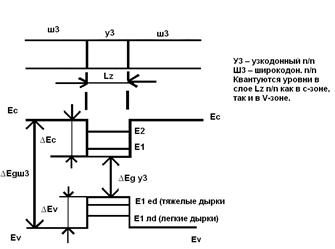
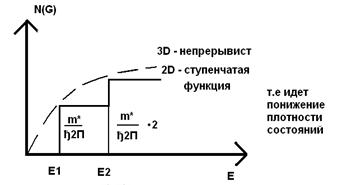
Плотность состояний N_c^2D

Дата добавления: 2014-01-07