Метод покоординатного спуска

Методы спуска

Методы минимизации функций многих переменных

Основная идея методов спуска состоит в том, чтобы построить алгоритм, позволяющий перейти из точки начального приближения 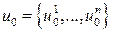в следующую точку таким образом, чтобы значение целевой функции приблизилось к минимальному.

Этот метод является редукцией поиска функции многих переменных к последовательности поиска минимумов функции одной переменной. Пусть – начальное приближение к минимуму Φ(u).

Рассмотрим 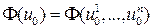как функцию одной переменной u₁ при фиксированных остальных и находим одним из приведенных методов поиска минимума функции одной переменной.

Полученное значение u₁, доставляющее минимум Φ(u₁), обозначим; при этом

.

Далее, при фиксированных значенияхищем

как функции от u₂; соответствующее значение u₂ обозначим; при этом

Этот процесс продолжаем аналогичным образом и для оставшихся координат; в результате получим

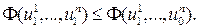
Таким образом, переходим из точки u ₀ в точку u ₁. Этот процесс повторяется до тех пор, пока не будет выполнено условие выхода из итераций, например:

где ε > 0 — заданная точность.

Рассмотрим методы оптимизации 1-ого порядка.

Из курса математики известно, что направление наибольшего возрастания функции характеризуется ееградиентом. Если критерий оптимизации задан уравнением: f(х₁,x₂,…x_n), то его градиент в некоторой точке О (из области определения функции) определяется вектором:

.

Известно, что направление вектора градиента совпадает с направлением наибольшего возрастания функции f в данной точке. Противоположное направление - это направление наиболее крутого убывания. Если критерий оптимизации задан аналитически, то вычисление градиента не представляет принципиальных трудностей. Однако, при оптимизации технологических систем критерий оптимизации, как правило задан в виде неявной функции.

В этом случае частные производные в точке O находят приближенными методами

,

где Δ - бесконечно малое приращение (1-5% от значения i - ой переменной).

Наряду с определением градиентного вектора основным вопросом, решаемым в методах градиента, является выбор шага движения по градиенту. Выбор величины шага в значительной степени зависит от вида поверхности. Если шаг слишком мал, это потребует продолжительных расчетов. Если наоборот размеры шага слишком велики, можно проскочить оптимум.

Метод градиента. Опишем принцип использования метода градиента на примере функции двух переменных f= f(Х₁, Х₂).

Этот принцип без изменения переносится на любое число переменных. Рассмотрим двумерную задачу (рис. 5.8)

Рис. 5.8.

Пусть в начальный момент значения X₁ и Х₂ соответствуют точке М₀ (см. рис. 5.8). Цикл расчета начинается с серии пробных шагов. Сначала величине X₁ дается небольшое приращение Δ > 0, причем в это время Х₂ неизменно. Затем определяется полученное при этом приращение Δ f, величины f, которое можно считать пропорциональным значению величины частной производной. Далее производится приращение величины X₂. В это время X₁ - const. Получаемое при этом приращение величины f является мерой другой частной производной. После нахождения составляющих градиента делается рабочие шаги в направлении вектора градиента, если стоит задача определения максимума и в направлении противоположном, если решается задача поиска минимума.

i =1, 2, k = 0, 1, 2,..., (5.3)

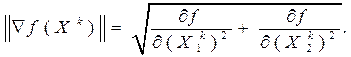
Таким образом определяются новые значения X₁ и Х₂, соответствующие точке М1. После каждого рабочего шага оценивается приращение Δ f величины f. Если Δ f >0 при поиске максимума или Δ f <0 при поиске минимума, то движение происходит в правильном направлении, иначе необходимо уменьшить величину шага. В качестве примера рассмотрим задачу поиска минимума функции: f( X)= X ₁²+25* X ₂².

Примем величину шага h =1, Δ X₁ = Δ X ₂ = 0.05. В качестве исходной точки поиска возьмём точку X ⁰ =(2,2)^T .

Поиск минимума осуществляем следующими этапами (см. табл. 5.1):

Таблица 5.

Шаг	X1	Х2				S1^k	S2^k	f
			4.050	101.25	101.250	-0.040	-0.999	104.00
	1.960	1.001	3.970	51.30	51.453	-0.077	-0.997	28.89
	1.883	0.004	3.816	1.45	4.082	-0.035	-0.355	3.55
	0.948	-0.351	1.94	-16.30	16.416	-0.119	0.993	3.98
Величина Δf>0,поэтому уменьшаем шаг вдвое.
0.5	1.416	-0.174	2.882	-7.45	7.988	-.0180	0.466	2.76
0.5	1.236	0.292	2.552	15.85	16.049	-0.079	0.494	3.66
Величина Δf>0,поэтому уменьшаем шаг вдвое.
0.25	1.326	0.059	2.702	4.20	4.994	-0.135	-0.21	1.84

Метод Коши (наискорейшего спуска или крутого восхождения).

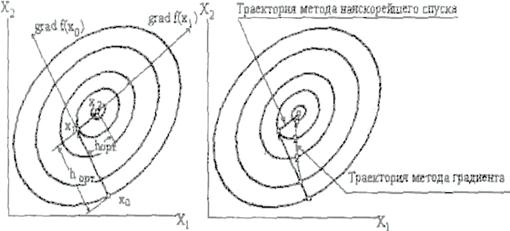
При использовании градиентного метода в задачах оптимизации основной объем вычислении приходится обычно на вычисление градиента целевой функции в каждой точке траектории спуска. Поэтому целесообразно уменьшить количество таких точек без ущерба для самого решения. Это достигается в методе Коши (наискорейшего спуска). Согласно этому методу, после определения направления поиска оптимума в начальной точке, в этом направлении делают не один шаг, а двигаются до тех пор пока происходит улучшение функции, достигая таким образом, экстремума в некоторой точке. В этой точке вновь определяют направление поиска (с помощью градиента) и ищут новую точку оптимума целевой функции и т.д. (см. рис. 5.9). В этом методе поиск происходит более крупными шагами, и градиент функции вычисляется в меньшем числе точек(см. рис. 5.9). Заметим, что метод наискорейшего спуска сводит многомерную задачу оптимизации к последовательности одномерных задач оптимизации, которые могут решаться, например, методом золотого сечения или половинного деления.

а) б)

Рис. 5.9. Метод наискорейшего спуска

а) Поиск максимума с выбором оптимального шага.

б) Сравнение с методом градиента.

Величину шага h можно определить из условия минимума f (X_k+h^kS^k):

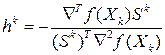
Пример. В качестве примера рассмотрим задачу поиска минимума функции:

f(X)=X₁²+25X₂².

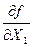
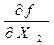
Этап	Шаг h^k	X1	Х2			f
				4.050	101.25	104.00
	2.003	1.92	-0.003	3.84	-0.15	3.19
	1.85	0.07	0.07	0.14	3.5	0.13
	0.07	0.07	-0.000			0.0049

Дата добавления: 2014-01-07