Метод сопряжённых градиентов

Квадратичная целевая функция n независимых переменных, имеющая минимум, может быть минимизирована за n шагов (или менее), если шаги предпринимаются в так называемых сопряжённых направлениях.

Вектор S₁ называют сопряжённым вектору S _0, если

,

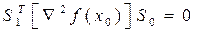где

Пример. Пусть f(X)=X₁²+X₂² -4, X₀ =(4,4),

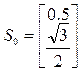
Обозначим координаты вектора S₁(S₁¹,S₁²). Тогда

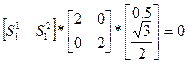
или

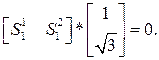
Отсюда S₁¹+√3*S₁² =0.

Добавим условие, чтобы длина вектора была равна 1:

Отсюда находим

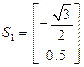
Вычислим градиент функции в исходной точке –

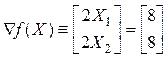
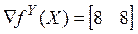
Находим:

,

,

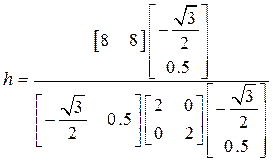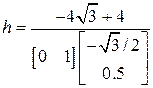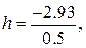
h= -5.86.

Тогда

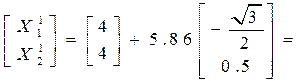
Метод вторых производных.

Метод Ньютона.

В соответствие с этим методом:

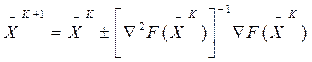
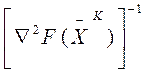
матрица обратная матрице Гессе.

Матрица Гессе

Пример. Найти минимум функции Розенброка:

.

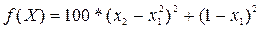В качестве исходной трчки поиска примем X=[-0.5 0.5}^T. f(X)=8.5

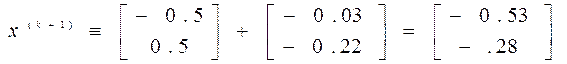
f(x)= 2.33

Мы рассмотрели основы методов оптимизации, для более глубокого их изучения можно обратиться к многочисленным литературным источникам, в том числе [16, 29, 34]. Ряд методов будет использован при выполнении практикума на ЭВМ.

Дата добавления: 2014-01-07