Лекция 6. Средние величины

Виды относительных величин

Правило действия с относительными величинами

Лекция 5. Абсолютные и относительные величины

В результате исследования статистической совокупности получают показатели, которые могут быть абсолютными или относительными.

Абсолютные величины – показатели, которые выражают разряды, уровни, объёмы и т.д. изучаемых явлений и процессов. Они всегда выражаются именованными числами (кг, м, шт, л). В этом их коренное отличие от относительных величин. Их единицы измерения называют натуральными.

Относительные величины – показатели, характеризующие количественные соотношения двух сопоставленных абсолютных и относительных величин. Относительные величины могут выражаться в коэффициентах (если за базу принимается единица), в процентах (если за базу принимается 100%), в промилле (если за базу принимается1000‰), а также через относительные натуральные сложные показатели (км/ч, руб/чел, чел/дней).

Все действия с относительными числами необходимо проводить, выразив их в виде коэффициентов, а не процентов. В расчётах пользоваться не темпами прироста, а темпами роста.

Относительное изменение во времени называется динамикой.

1. Относительная величина плановой динамики (планового задания) – отношение планового уровня текущего года к фактическому значению в предыдущем периоде.

2. Относительная величина выполнения плана – отношение фактического значения к плановому за один и тот же период.

3. Относительная величина динамики – отношение двух фактических значений текущего года к базисному.

Пример: Найти недостающие абсолютные и относительные величины

№ фирмы	А.фактическое оказание услуг за 2004 г.	2005 г.	относительные величины
плановое значение	фактическое значение	плановой динамики	выполнения плана	Динамики
	а	b	c	d/a	c/b	c/a
	20 21,05	31,5	32,4 22	110% 90% 105% 95%	109% 117% 103% 110%	120% 105% 108% 104,5%

Вспомогательные формулы: b=a*b/a; c=a*c/a; c=b*c/b; a=b:b/a; c/a=c/b*b/a; b/a=c/a*c/b

4. Относительная величина структуры – отношение каждого элемента ряда к итогу.

Пример:

№	выпуск продукции	относительная величина структуры
итог:		20:200=10% 30:200=15% 120:200=60% 30:200=15%   100%

5. Относительная величина координации – отношение каждого элемента ряда к элементу, принятому за базу сравнения.

Пример:

№	выпуск продукции	относительная величина координации
	120	20:120=16,7% 30:120=25% 120:120=100% 70:120=58,3%

6. Относительная величина сравнения – сопоставление двух объектов за один и тот же период.

7. Относительная величина интенсивности – в отличие от всех прочих имеет единицу измерения и представляет собой отношение двух разноимённых показателей.

Среди показателей, характеризующих статистические совокупности, важное место занимают средние величины.

Средняя величина – показатель, который даёт обобщённую (усреднённую) характеристику единиц изучаемой совокупности. В средней величине отражается то общее, что имеется в каждой единице совокупности.

Сущность статистической обработки методом средней величины заключается в замене индивидуальных значений признака их средним показателем. При этом общий объём совокупности остаётся неизменным.

Пример: есть данные о выработке 5 рабочих: 135, 141, 153, 159, 162. Определить среднюю выработку. .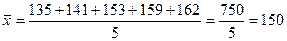

Средние величины, которые необходимо знать наизусть:

- средняя арифметическая;

- средняя гармоническая;

- средняя хронологическая;

- средняя квадратическая, кубическая;

- средняя геометрическая;

- структурные средние: мода, медиана.

1. Средняя арифметическая: чаще всего в статистике и социально-экономических исследованиях применяется арифметическая величина.

Средняя арифметическая простая рассматривается в случаях, когда значение признака повторяется один или одинаковое число раз в ряде распределения:

, где n -количество единиц совокупности.

Средняя арифметическая взвешенная применяется в случаях, когда каждое значение признака повторяется неодинаковое число раз, или частота ряда распределения превышает единицу хотя бы для одного признака:

, где f -вес.(сколько раз повторяется каждая еденица совокупности)

2. Средняя гармоническая: в ряде случаев бывают известны варианты (x) и произведения варианты на частоту (x∙f), в то время как сами частоты (f) неизвестны, тогда применяется средняя гармоническая, которая бывает простой и взвешенной..

Произведение x∙f выражается через сложный экономический показатель M (M = x∙f). Для расчёта средней величины, когда x∙f = M = 1, применяется средняя гармоническая простая: .
Если x∙f =M≠ 1, то для расчёта применяется средняя гармоническая взвешенная: .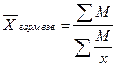

Средняя гармоническая – величина, обратная средней арифметической, из обратных значений признака.

Дата добавления: 2014-01-07