Полярна засічка

У полярної засічки вихідними даними є координати точки A і дирекційний кут напрямку AB (або координати пункту B), вимірюваними елементами є горизонтальний кут β і відстань S, а невідомими елементами – координати точки P (X, Y).

Для графічного рішення полярної засічки від напрямку AB відкладається кут β і проводиться пряма AQ, а потім навколо точки A описується окружність радіусом S в масштабі карти. Точка перетину прямої лінії та кола дасть потрібну точку P. Вирішимо полярну засічку аналітично. Дирекційний кут α лінії AР дорівнює 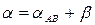. Запишемо рівняння прямої AP та кола радіуса S з центром в точці A:

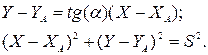(6.1)

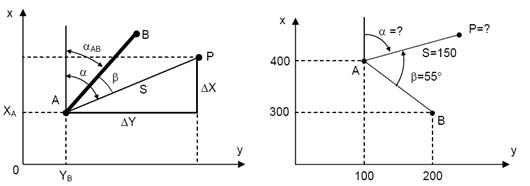
Рисунок 6.2 – Полярна засічка

Вирішуючи систему (6.1) методом підстановки і використовуючи відомі тригонометричні співвідношення, отримуємо однозначне рішення системи:

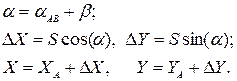(6.2)

За допомогою полярної засічки вирішується пряма геодезична задача – обчислення координат точки (XB,YB), якщо відомі координати точки (XA,YA), відстань між цими точками – SAB, а дирекційний кут дорівнює α. Пряма геодезична задача вирішується за формулами:

(6.3)

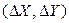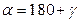Зворотня геодезична задача полягає в обчисленні дирекційного кута α і довжини лінії S, що з'єднує дві точки A і B з відомими координатами і Для отримання кута α можна обчислити кут і визначити квадрант, в який потрапляє точка . Якщо дирекційний кут , інакше .

Дата добавления: 2014-01-07